平衡树(“自平衡的二叉搜索树”)是一种在各种情景下常用的数据结构,其最常用的应用包括维护一个全序的集合,或者以一个全序的集合进行索引,或者维护一个序列。
平衡树
假设读者知道平衡二叉搜索树的一些基本常识。对于一个树结构而言,要么在叶子上储存数据,要么在每个结点储存数据,这样我们就有 Nodey 和 Leafy 的区分。
在 Leafy 结构中,每个叶子储存值,每个非叶结点是中间结点、只维护形态、必定有两个孩子;插入(删除)一个值时,除了插入(删除)一个叶子之外,还会额外插入(删除)一个非叶结点。我们分别把非叶结点和叶结点叫做内点和外点。可以发现,Leafy 二叉树的中序遍历一定是“外内外内外……内外”这样交替的。
在 Nodey 结构中,每个结点不仅储存值,还维护结构。每个结点可以有空指针孩子。这是大家一般熟悉的平衡树结构。对于每种 Nodey 结构,我们把所有空指针指向另一种维护值的东西,就可以方便地变成一个 Leafy 结构。
对于每个平衡树,我们可以放松它“储存有序元素”的限制,拿它来储存一个序列。在每个结点额外维护它的子树大小(对于 Leafy,子树叶子个数),就可以利用一次平衡树查找来随机访问下标,具有复杂度 \(O(\log n)\) 。
例如上图储存了序列 \([9, 9, 8, 2, 4, 4, 3, 5, 3]\) 。注意到,对于一棵 Leafy 的树,如果其外点维护了一个序列,那么其内点刚好形成了一个“内点的序列”,和一棵 Nodey 的树相同。
串接与拆分运算
序列的串接
\(\def\defopname#1{{\newcommand{#1}{{\operatorname{#1}}}}}\def\opname#1{{\defopname{#1}\mathbf{#1}}}\)很自然地,我们会想到串接(\(\opname{merge}\))两个序列;比如说对 \(u=[5, a, 1]\) 串接上 \(v=[s, a, 3, d]\) 得到 \(u\cdot v=[5,a,1,s,a,3,d]\) 。如果我们加强限制为二叉查找树,那就是给出两个集合 \(S,T\) ,每个 \(S\) 的元素都小于 \(T\) 的任意元素,我们要得到集合 \(S\cup T\) 。下文我们只讨论序列。注意到这在 Nodey 和 Leafy 的树上有不同的行为:
- 对于两个表示为 Nodey 树的序列,\(\merge\) 就是把点集想办法串起来。
- 对于两个表示为 Leafy 树的序列,\(\merge(v,w)\) 的时候我们需要新建一个中间结点 \(t\) ,内点的序列会实际变为 \(v\cdot [t]\cdot w\) 。(注意内点个数总是外点个数减一。)
序列的拆分
同样,我们可以把一个序列拆(\(\opname{split}\))成两个:\((l,r)\gets\split(v, k)\) 表示把 \(v\) 拆分成前 \(k\) 个和后 \(|v|-k\) 个,分别放到 \(l,r\) 中。这里的拆分标准可以不是数量、而是任意可以查找的单调谓词,比如说对于一个集合来说可以定义 \((l,r)\gets\text{split by value}(v,k)\) 表示 \(l\gets\{x\mid x\in v,x\leq k\}\) ,\(r\gets\{x\mid x\in v,x> k\}\) 。
三元形式
如果我们希望在 Nodey 树中表示 Leafy 的 \(\merge, \split\),这两个运算实际上有三元形式。
- \(\merge(v,x,w)\) 表示 \(v\cdot [x]\cdot w\) 或 \(v\cup\{x\}\cup w\) 。
- \((l,x,r)\gets\operatorname{split by size}(v, k)\) 表示将其拆分成前 \(k-1\) 个、中间一个、后 \(n-k\) 个。
- \((l,x,r)\gets\operatorname{split by element}(v,x)\) 表示将其拆分成中序遍历上在 \(x\) 之前的、\(x\) 自身、\(x\) 之后的。
- 当然也可以定义其他种类的拆分。
实现
在算法竞赛中,Splay 和 Treap 的串接比较为人所熟知。具体来说,Nodey Splay 在串接 \(\merge(v,w)\) 时只需要找到 \(v\) 的最右元,将其 splay 到根,然后将 \(w\) 插入为它的右孩子;Nodey Treap 有一个非常知名的“非旋转”递归合并,在此就不展示了,可以利用搜索引擎搜索 fhq treap 找到。
Treap
考虑一般的旋转 Treap,我们实现它的一个 Leafy \(\merge\):对于 \(v,w\) ,我们新建一个结点 \(t\),给它一个随机的权值,然后将 \(v,w\) 分别设为它的左右孩子。此时堆性质有很大概率已经被破坏了,我们用旋转的方法将 \(t\) 根据权值不断往下旋转,直到堆性质得到重新满足。注意到这是一个(期望)复杂度为 \(O(\log n)\) 的正确算法,保证了外点之间的相对顺序。对于 Nodey 的 Treap,我们可以使用同样的方法进行 \(\merge\) ,只是让这个结点具有权值 \(-\infty\) (假设是大根堆),这样它一定会旋转到叶子,然后将它删除即可。
我们可以用非常相似的思路实现 \((l,r)\gets\split(v, k)\)。不妨先实现 Leafy 版本。利用 \(k\),我们可以找到 \(l\) 的最右结点(第 \(k\) 个)和 \(r\) 的最左结点(第 \(k+1\) 个);它们在中序遍历上一定恰好隔着一个内点,也就是它们的最近公共祖先。将这个点的权值设为 \(+\infty\),然后进行一系列旋转维护堆性质,它就会被旋转到根,此时它的左右孩子就分别是 \(l,r\),将根自身删除即可。Nodey 版本,我们额外插入一个结点在第 \(k\) 个之后,然后做上述过程。\(\text{split by value}\) 的过程可以类推。
AVL 树
对于 Leafy AVL,不妨假设 \(\merge(v,w)\) 的时候 \(v\) 的高度比较大。在 \(v\),\(v\) 的右孩子,\(v\) 的右孩子的右孩子…这个序列中,相邻两个的高度差至多是 \(2\) ,因此其中至少有一个 \(y\) 满足 \(0\leq \text{height}(y)-\text{height}(w)\leq 1\)。设 \(x\) 是 \(y\) 的父亲,我们把 \(x\) 的右孩子替换成新结点 \(t\) ,然后让 \(t\) 的左右孩子分别是 \(y, w\)。由 \(y\) 的定义,\(\text{height}(t)=\text{height}(y)+1\),此时 \(x\) 的平衡性质可能被破坏(因为它的右孩子高度增加了 \(1\) )。我们做一个近似于插入的平衡调整即可。对于 Nodey AVL,做完全相同的操作,然后把新结点删掉。注意到这一算法的复杂度是 \(O\big(|\text{height}(v)-\text{height}(w)|\big)\) 。
举个例子:我们要把这两棵树合并,合并的中间节点是 \(50\) :
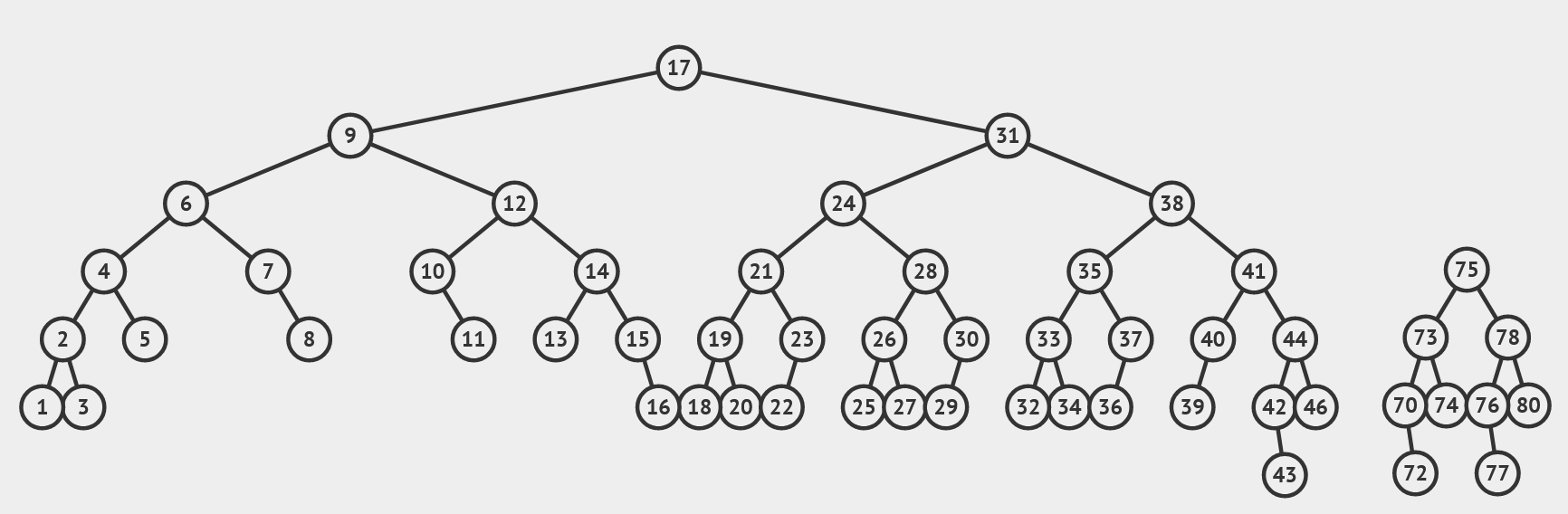
我们从 \(17\) 的右链中找到和 \(75\) 的高度相差不超过 \(1\) 的,也就是 \(41\),把它和它父亲之间断开,然后把 \(50\) 接上去:
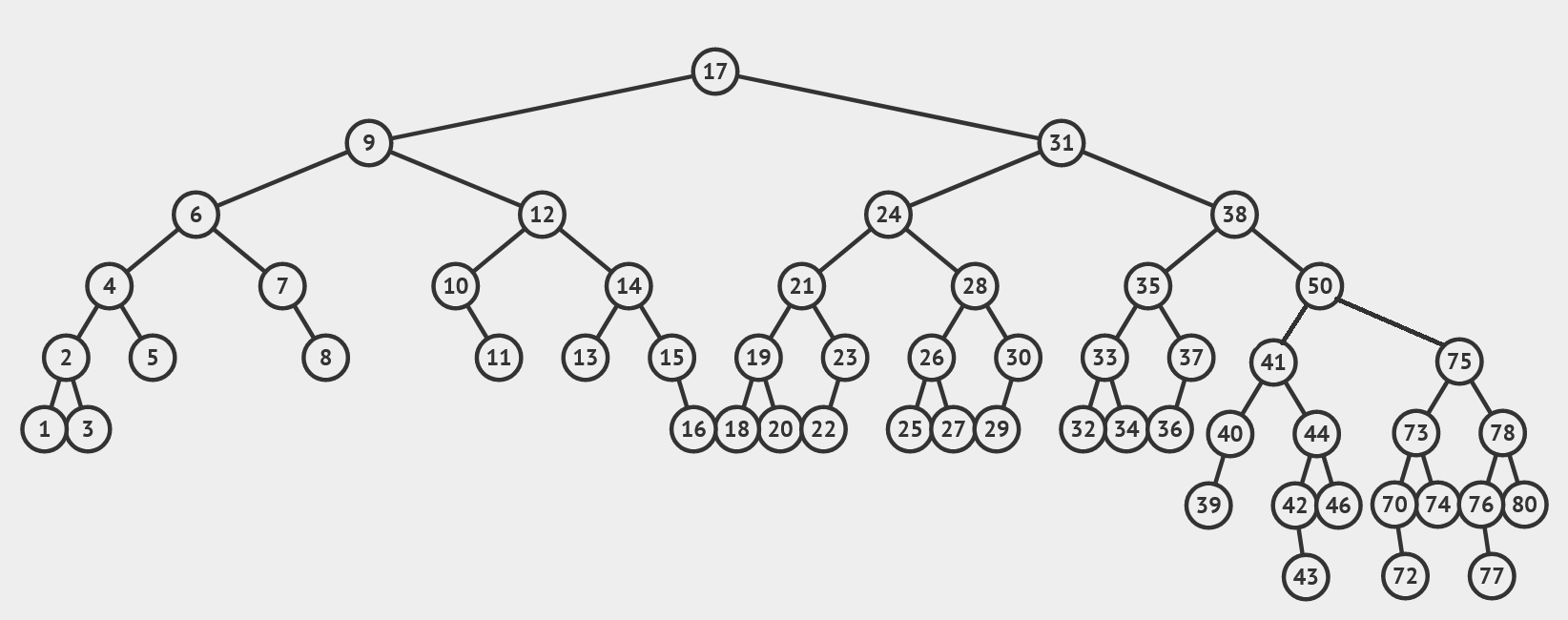
然后从 \(50\) 开始向上扫描,发现 \(38\) 的高度性质不满足,需要旋转。这和插入一个节点之后的过程非常接近,就不画了。
\(\split\) 对于 Nodey 和 Leafy 的版本是差不多的,我们以 Leafy 为例。我们先利用 \(k\) 找到待删除临时结点 \(t\) ,然后将这一结点到根的整条路径拿出来,不妨设为 \(v=v_0, v_1, \cdots,v_n = t\)。利用它们之间边的方向,我们可以判断出每一个 \(v_i\) 会在答案的哪部分中——如果 \(v_{i+1}\) 是 \(v_i\) 的右孩子,那么 \(t\) 在 \(v_i\) 的右子树中,因此中序遍历 \(v_i\) 和它的整个左子树在 \(t\) 的左边,因此它是答案的 \(l\) 的一部分;否则 \(v_i\) 会是 \(r\) 的一部分。此外,\(t\) 的左右孩子分别在左右这两部分。分别把它们记作 \([L_0, L_1, \cdots, L_p];\;[R_0,R_1,\cdots,R_q]\)。举个例子。
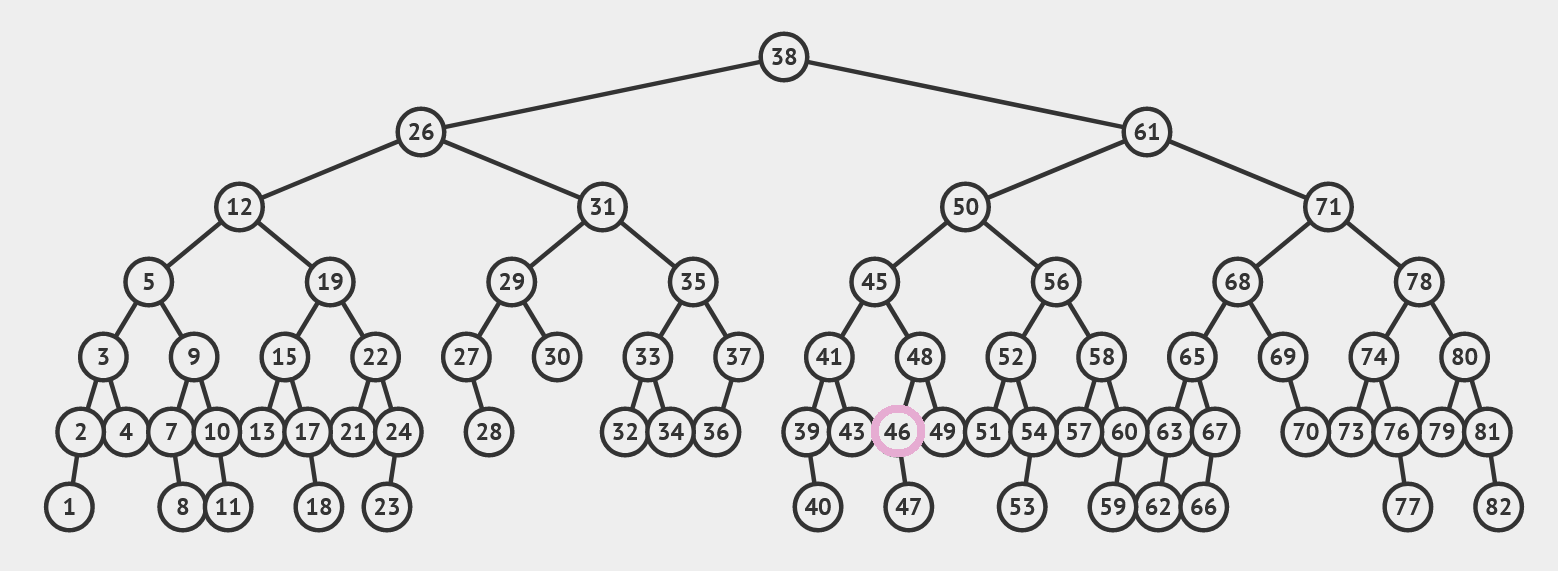
假设我们要 \(\split\) 的点是 \(46\) ,那么把它到根的所有路径切开,得到 \([v_i]=[38,61,50,45,48,46],\,[L_i]=[38, 45],\,[R_i]=[61,50,48,47]\) 。
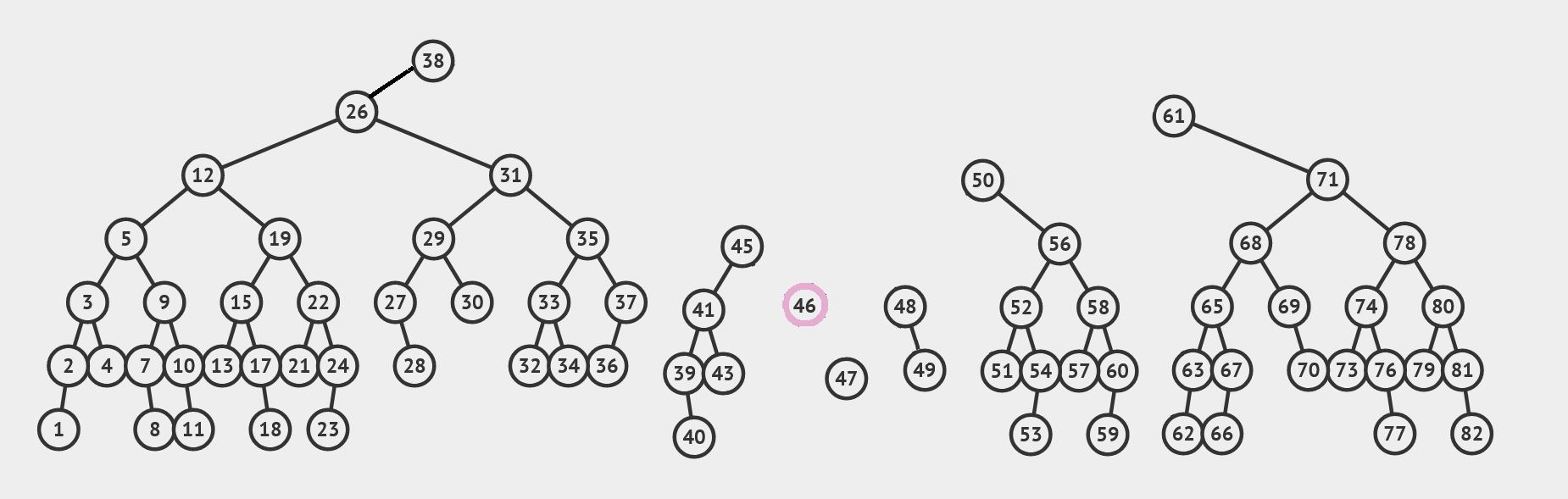
我们把它们相邻之间的边断开,让它们成为 \(p+q\) 个孤立的树(和一个孤立的点 \(t\))。对于每一个 \(L_i\) ,它都是没有右孩子的树。我们把他们的左孩子分别拿出来,记作 \(\ell_0, \cdots, \ell_p\),把 \(L_i\) 和 \(\ell_i\) 之间的边断开。注意到每个 \(\ell_i\) 都是平衡的 AVL 树。那么我们的答案 \(l\) 的中序遍历会是 \(\ell_0 \cdot [L_0] \cdot \ell_1 \cdot [L_1] \cdots \ell_p \cdot [L_p]\)。我们可以使用我们的三元 \(\merge\) ,使用 \(L_k\) 作为中间结点,将它们逐一合并起来。对 \(r\) 是对称的。
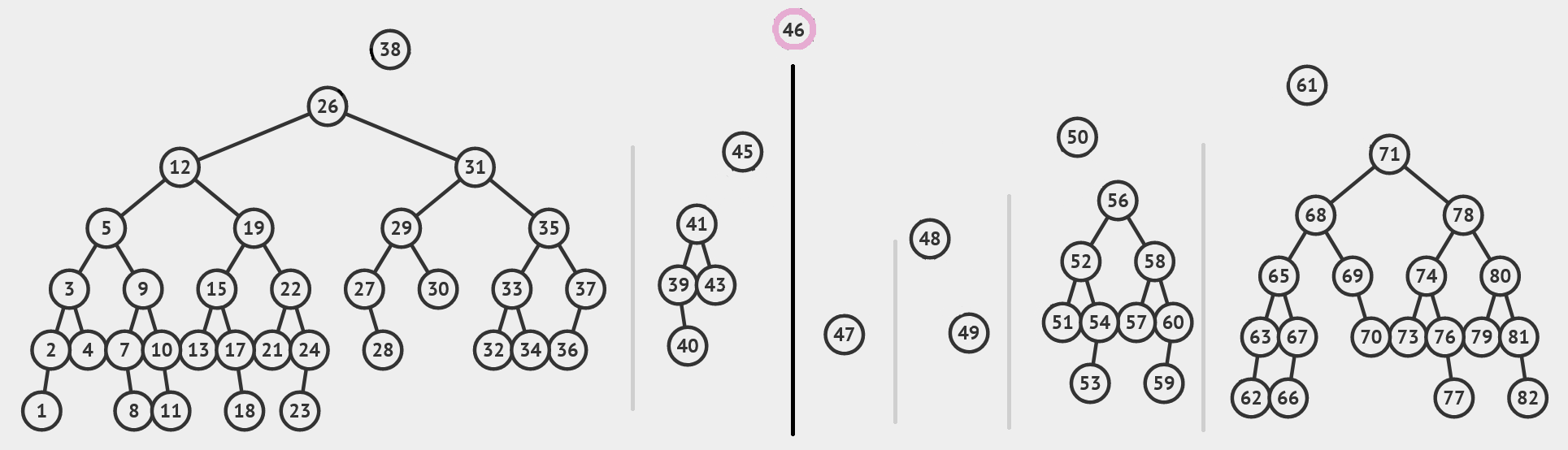
我们的 \([L_i]=[38, 45],\,[R_i]=[61,50,48,47]\) ,而 \([\ell_i]=[26,41],\,[r_i]=[71,56,59,\varepsilon]\) ,其中 \(\varepsilon\) 表示空树。我们最终把它这样合并起来:
我们在合并它们的过程中这个东西的复杂度就会是 \(|\operatorname{height}(\ell_0)-\operatorname{height}(\ell_1)|+|\operatorname{height}(\ell_1)-\operatorname{height}(\ell_2)|+\cdots\) 注意到 \(\ell_i\) 们的高度是单调的,因此总复杂度依然是 \(O(\log n)\) 。
B树,红黑树(以及 WBT,以及其他一些局部的平衡树)
考虑B树,和 AVL 有非常大的相似性。\(\merge\) 时,我们考虑根结点往右走的链中的所有结点的是单调递降的,因此可以找到一个和另一棵树高度一样的,然后利用中间结点把它们拼到一起,然后就像插入一样去维护平衡性。\(\split\) 时,使用完全一样的方法拆分,但是一个多个孩子的结点需要拆成若干个。
对于红黑树,将它理解成 \(\text{order}=4\) 的B树,那么就是考虑“黑高度”去找结点。拆分的时候为了维护性质需要把 \(L_i,R_i\) 的根结点染黑。
如果平衡树是用子树大小而不是高度来平衡的,那么在 \(\merge\) 右链找点时找大小相差不超过两倍(或者若干倍)的,复杂度是 \(O\left(\log\frac{\mathrm{size}(v)}{\mathrm{size}(w)}\right)\) ,同样可以证明 \(\split\) 的复杂度。
对于 Treap,你同样可以用这一方法来维护,\(\merge\) 第一步的右链找结点要按权值去寻找。它具有期望复杂度。
注意到上述的东西是可以利用 Path-Copy 进行可持久化的。
精细的复杂度分析,以及 Finger Search
我们假设你的平衡树维护了父亲指针,并且额外保存了整棵树的最左和最右结点,那么对于上述 AVL、红黑树、WBT 合并的过程,你可以从根方向和叶子方向挑一个近的来找,那么找到一个被替换的结点 \(y\) 的复杂度是 \(\min\{|h_a-h_b|,h_a,h_b\}\) ,也就是 \(O \left(\min\!\left\{\log n,\log m,\left|\log\frac nm\right|\right\}\right)\) 。但找到替换结点之后,我们需要遍历它的祖先来维护平衡性。我们假设这一步具有优秀的复杂度,那么,对于 \(\split\),从一棵 \(n\) 个点的树中切出前 \(t\) 个结点也可以具有复杂度 \(O \left(\min\!\left\{\log n,\log (n-t)\right\}\right)\) 。
事实上,这种比较“局部”的操作有一个名字,叫做 Finger Search。如果某一操作从一个位置到另一个位置的时间复杂度不是和整棵树的大小相关,而是和他们之间的距离相关,那么称这一操作具有 Finger Search 复杂度;换句话说,上述的 \(O(\log t)\) 就是 Finger Search 复杂度。Splay 天然具有 Finger Search 复杂度 \(O(\log t)\)。
如果一种二叉搜索树可以以 Finger Search 复杂度 \(O(\log t)\) 进行 \(\merge\) 和 \(\split\),那么它可以以 \(O(m \log \frac nm)\) 的复杂度进行两个集合的并集:假设较小的集合的大小是 \(m\) ,这 \(m\) 个元素分别在较大的集合中具有位置 \(a_1, \cdots, a_m\),那么把大的集合拆开、小的集合一个个加进去、然后合并回去的复杂度就是 \(\sum\log\left(a_{i+1}-a_i\right)\),显然在均匀时取到最大。注意到,基于元素比较的所有算法中这是最优的,因为复杂度下界是 \(\log{{n+m}\choose{m}}=O(m\log \frac nm)\)。
那么,把 \(n\) 个初始大小为 \(1\) 的集合以任意顺序做并集操作合并起来的复杂度就是 \(O(n\log n)\),也就是俗称的“启发式合并”。
假设的证明
这一切都建立在“遍历祖先维护平衡性具有优秀的复杂度”这一假设下。对于 Treap,它的期望复杂度满足这一假设。对于红黑树和B树而言,它的平衡操作比较局部,我们通过对“(2,4)-B树每个结点的孩子数和 \(\text{order}\) 的差”或者“红黑树的红色结点个数”进行记账均摊分析,就可以证明这一假设。对于 AVL,我们通过对“左右孩子高度差不为零的结点个数”进行记账均摊分析。
这个东西也是可以可持久化的。由于你要“最左和最右结点”,我们索性把最左链和最右链上下颠倒地拿起来(想象:一只手拿着最小元,一只手拿着最大元,然后放开根结点,让整棵树落下来)。这个就是 Finger Tree 了,利用一些技巧可以做到完全函数式的 Finger Search 复杂度的 \(\merge, \split\) 。
致谢
感谢 myc 同学和我对相关内容进行了讨论,给了我写这篇文章的动力。
感谢 lxl 学长的捉虫。