无标号图编码

背景：这是算分小班课的一个 challenge，出题人是 kczno1。可以戳此看我课内分享时的讲稿 pdf。

题意

这是一道通信题。你需要写两个代码，一个编码器，一个解码器。

你的编码器需要把一个尽可能长的比特串编码成一个 \(N=100\) 个点的无标号无向图。
交互库会打乱这张图的点和边的排序。
你的解码器需要把这张图还原回比特串。

算法必须是确定性、100% 正确的。你的程序需要在合理的时空限制内运行（在一颗当代的工作站 CPU 上，1s 时间限制，2GB 空间限制）。

思考

我们假设编码函数是 \(g=e(s)\)，解码函数是 \(s=d(g)\)，其中 \(s\in S=\{0,1\}^n\)， \(g\in e(S)\)。考虑集合在算法是正确、完全确定性的基础上，我们知道 \(d(-)\) 可以用来做图同构；\(g_1\cong g_2\iff d(g_1)=d(g_2)\)，因此我们相当于解决了编码函数的值域 \(e(S)\) 内的图同构问题，这意味着这个集合不会特别大。

ztr 的观点：“对于 90% 的图适用的图同构算法”其实应当是存在的？

我们知道 \(e(S)\) 不会多于 \(N\) 个点的无标号图个数 \(a(N)\)。注意到 A000088 提供了一个渐近式子；我们可以直接使用其一阶项 \(a(N)\approx \frac{2^{N\choose 2}}{N!}\)，那么我们的 \(\ell\) 就有一个上界 \(\ell\le \lfloor\log_2 a(N)\rfloor =4425\)。

算法想法

首先一张有标号图可以很自然地编码 \(v\choose 2\) 比特的信息，那么我们很自然的想法就是先搞一张有标号图 \((V_a,E_a)\) ，然后在上面加一些点 \(V'\)，然后用 \(V'\) 与 \(V_a\) 之间的边去恢复 \(V_a\) 内部的标号。

一个很自然的想法是二进制编码。设 \(a=|V_a|\)，我们取 \(b=\lceil \log_2 a\rceil\) 个点，设 \(V_b=\{\mathfrak b_0,\cdots,\mathfrak b_{b-1}\}\) ，然后对于 \(V_a\) 内标号为 \(i\) 的点，它和 \(\mathfrak b_j\) 连边当且仅当 \(i\) 的第 \(j\) 个二进制位是 \(1\)。

现在我们需要让 \(V_b\) 内部的点相对能区分出来。所有 \(V_b\leftrightarrow V_b\) 的边形成的子图称作 \(G_b\)，只要这张小图没有自同构，我们就可以把 \(V_b\) 内部的点区分出来。例如 \(b=7\) 的时候我们可以采取如下这张图：

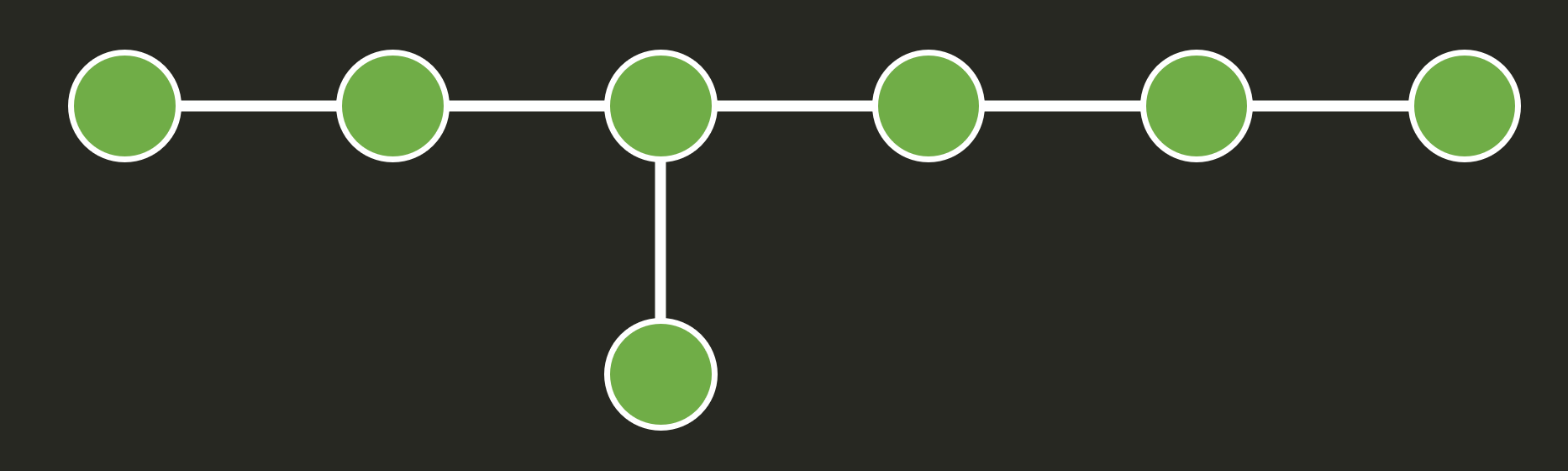
那么我们只需要区分出哪些点是 \(V_a\)，哪些是 \(V_b\) 就可以了。我们再添加一个点 \(u\)，让它和所有 \(V_b\) 中的顶点连边；这样我们只要找到 \(u\)，我们就可以找到 \(V_b\) 、进而区分出 \(V_b\) 的内部、进而给 \(V_a\) 进行标号。为了找到顶点 \(u\)，我们再添加一个顶点 \(w\)，让它和 \(V_a\cup V_b\) 连边，这样我们只要找到顶点 \(w\)，我们就可以找到顶点 \(u\) （因为这是它唯一没有连边的顶点）。但顶点 \(w\) 是容易找的；它一定是度数最大的顶点。

因此，我们设 \(V=V_a \cup V_b \cup \{u,w\}\)，\(V_a\) 内部按 \(a\choose 2\) 比特的信息连边，\(V_a\leftrightarrow V_b\) 按二进制标号连边， \(V_b\) 内部按特殊小图连边，\(u\) 连所有 \(V_b\)，\(w\) 连所有 \(V_a,V_b\) 即可。

这其实就是 JOI 2018 SC 的“航空路線図”一题，可以在上述链接中找到题解与代码。利用这一算法，我们可以发现 \(a=91,b=7\)，我们可以编码 \({91\choose 2}=4095\) 比特的信息。

在算分小板内部的竞赛内，这已经是第一了；但我们还是想问，

优化 #1

注意到我们把一个 \(a\) 个点的有标号图编码成了一个 \(a+\log a+2\) 个点的无标号图。这个 \(2\) 看起来就很假，我们能不能想办法把它优化成 \(1\) 呢？答案是可以的。注意到我们解码算法的第一步一定只能用一些全局的性质，比如说度数序列。那么我们如果要用度数序列来区分出两种东西，一个很自然的想法就是利用度数的奇偶性。

我们考虑在连完了 \(V_a\cup V_b\) 的边之后，这些 \(a,b\) 类的点，有些度数是奇数、有些是偶数。通过添加一个新顶点 \(w\)（以及让它连一些边），我们可以让所有 \(V_a\) 点度数为偶数、\(V_b\) 点度数为奇数。注意到此时 \(a=92,b=7\)，因此 \(w\) 的度数一定是奇数。

解码的时候，我们会找到所有 \(b\) 类的点加上 \(w\)。对于所有 \(b\) 类的点，我们完全能精确地知道他们会连哪些边，因此我们完全可以预测新点会和哪些 \(b\) 点连边。观察一下就会得到这样一张小图：

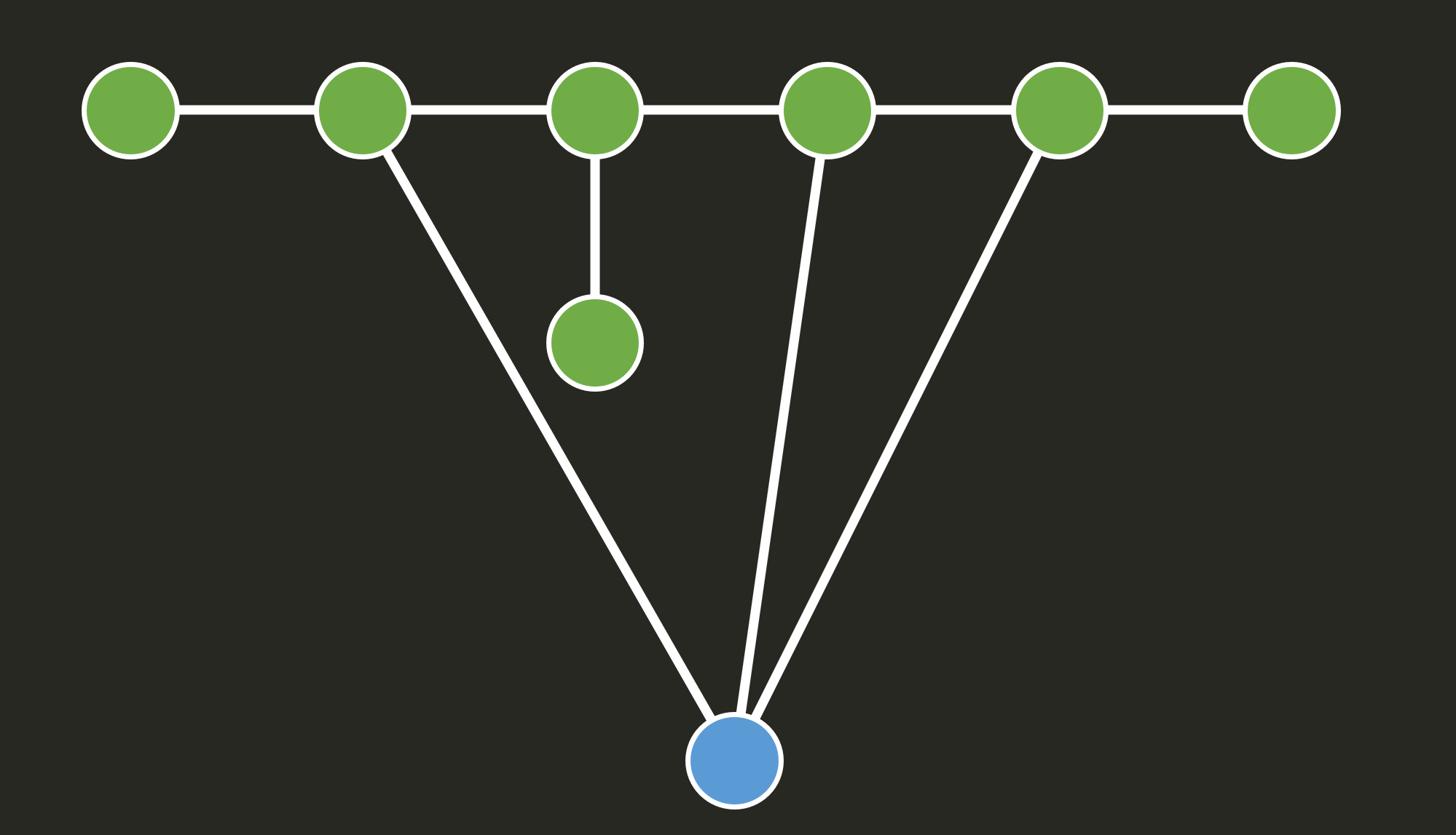
观察可知这张图是没有自同构的，因此我们可以找出每个 \(\mathfrak b_i\) 然后继续正常解码。

这样处理之后，我们就可以在 \(100\) 个点的无标号图中编码（内嵌）一个 \(92\) 个点的有标号图，进而编码 \({92\choose 2}=4186\) 比特的信息。这已经有了一定的改善；但我们还是想问，

优化 #2

我们在二进制编码 \(V_a\leftrightarrow V_b\) 的时候，把 \(0, 1, \cdots, 91\) 每个都当成了一个七位的二进制数；但实际上我们浪费了七位的二进制数空间，只使用了其中的一部分。我们考虑这些数字其实可以是 \(0, 1, \cdots, 127\) 之间的任意 \(92\) 个，只要把它们从小到大排序好 \(a_0<a_1<\cdots<a_{91}\)，然后

原本是：对于 \(V_a\) 内标号为 \(i\) 的点，它和 \(\mathfrak b_j\) 连边当且仅当 \(i\) 的第 \(j\) 个二进制位是 \(1\)；
更改为：对于 \(V_a\) 内标号为 \(i\) 的点，它和 \(\mathfrak b_j\) 连边当且仅当 \(a_i\) 的第 \(j\) 个二进制位是 \(1\)。

这个 \(\{a_0,\cdots,a_{91}\}\) 是 \(\{0, \cdots, 127\}\) 内的任意一个大小为 \(92\) 的集合，因此我们这里可以额外多出 \(\log_2 \binom{128}{92}\approx 106\) 比特的信息。我们只需要写一个子集的字典序排序计算即可，这是一个简单的 DP 任务。

点此展开代码

// U2048 是大整数类；它的 operator[] 是获取某一个二进制位。
// C 是 U2048[][] 类型，表示组合数。
U2048 ord2set(U2048 x, int n, int k) {
    U2048 ans = 0;
    while (n > 0) {
        u32 bit = 0;
        if (k == 0 || C[n - 1][k - 1] <= x) {
            if(k > 0) {
                x -= C[n - 1][k - 1];
            }
            bit = 0;
        } else {
            bit = 1;
            --k;
        }
        ans[--n] = bit;
    }
    return ans;
}

U2048 set2ord(U2048 x, int n, int k) {
    U2048 ans = 0;
    while (n > 0) {
        u32 bit = x[n - 1];
        if (bit) {
            --k;
        } else {
            if (k > 0) {
                ans += C[n - 1][k - 1];
            }
        }
        --n;
    }
    return ans;
}

但这样会引入一个问题：我们在解码那 \(8\) 个点的小图的时候，上面那张固定的小图依赖 \(V_b\) 的度数序列；但改变 \(V_a\) 的标号数字会改变 \(V_a \leftrightarrow V_b\) 的边，这会改变 \(V_b\) 的度数（的奇偶性），进而改变 \(w\leftrightarrow V_b\) 的连边。但我们可以找若干张不同的 \(G_b\)，按照不同的 \(a\) 序列选选择不同的 \(G_b\)；简单来说，

如果 \(w\leftrightarrow V_b\) 的边比较多，我们选择一个比较稀疏的 \(G_b\)，这样 \(w\) 是这些点里面度数最大的；
如果 \(w\leftrightarrow V_b\) 的边比较少，我们选择一个比较稠密的 \(G_b\)，这样 \(w\) 是这些点里面度数最小的。

利用这个技巧，我们可以额外编码 \(\log_2 \binom{128}{92}\approx 106\) 比特的信息，把我们的信息总量加到了 \(\left\lfloor \binom{N-b-1}{2}+\log_2 \binom{2^b}{N-b-1}\right\rfloor=4292\) 比特。已经十分接近上界 \(4425\) 了，但我们还是想问，

优化 #3

还是可以的。注意到刚才这个式子 \[ \ell=\left\lfloor \binom{N-b-1}{2}+\log_2 \binom{2^b}{N-b-1}\right\rfloor \] 这个式子真的在 \(b=\lceil \log_2 N\rceil\) 的时候最优吗？直觉感觉不太对啊，那我们就把它扔到 Mathematica 里面跑一下。

还真就不对。可以发现，在 \(b=11\) 的时候上述式子取到最大值。修改上述算法，我们需要重新设计小图。考虑由于 \(w\leftrightarrow V_b\) 的边的数量不同，我们考虑：

在 \(w\leftrightarrow V_b\) 的边的数量至少为 \(6\) 的时候使用下面这张图：
在 \(w\leftrightarrow V_b\) 的边数量不超过 \(5\) 的时候使用这张图的补图。

实现细节上，注意到此时我们的小 DP 需要一个 \(2048\) 级别的组合数，因此需要一个比较大的高精度库；但时空效率不成问题。

那我们现在就能做 \(\ell=4347\) 了，我们还是想问，

分析

注意到我们现在能做 \(4347\)，但理论上界是 \(4425\)，这里的相差已经非常接近了。考虑 \(N\to\infty\) 的渐近意义下，（即使不用这三个优化，）这个比特利用率大概在 \(1-\Theta\left(\frac{\log N}{N}\right)\) 量级，是 \(\to 1\) 的。

代码

代码中有大量的中间产物是没有用到的，包括用爆搜找小图什么的，可以无视其中没用到的代码。

点此展开完整代码

#include "bits/stdc++.h"
using namespace std;

constexpr int graph_size = 100;

using EdgeListGraph = vector<pair<int, int>>;
using SparseGraph = vector<vector<int>>;

std::random_device rd;
std::mt19937 mt{114514};

struct EncoderParameter
{
  int labeled_n;
  int unlabeled_n;
  int lg2;
  int tab_len;
};

struct EncoderResult
{
  EncoderParameter param;
  EdgeListGraph g;
};

SparseGraph graph_cast(int n, const EdgeListGraph &ge) {
  SparseGraph g(n);
  for (auto x : ge) {
    g[x.first].push_back(x.second);
    g[x.second].push_back(x.first);
  }
  return g;
}

EdgeListGraph graph_cleanup(EdgeListGraph g) {
  for (auto &x : g) {
    if (x.first > x.second) swap(x.first, x.second);
  }
  sort(g.begin(), g.end());
  auto it = unique(g.begin(), g.end());
  g.resize(it - g.begin());
  return g;
}

EdgeListGraph graph_cast(const SparseGraph &gd) {
  EdgeListGraph ge;
  for (int x = 0; x < gd.size(); ++x) {
    for (auto y : gd[x]) {
      if (x < y)
        ge.push_back({x, y});
    }
  }
  return ge;
}

vector<int> deg_sequence(int n, const EdgeListGraph &g) {
  vector<int> ans(n, 0);
  for (auto x : g) {
    ans[x.first] += 1;
    ans[x.second] += 1;
  }
  return ans;
}

EdgeListGraph complete_graph(int n) {
  EdgeListGraph ans;
  ans.reserve(n * (n - 1) / 2);
  for (int i = 0; i < n; ++i) {
    for (int j = i + 1; j < n; ++j) {
      ans.push_back({i, j});
    }
  }
  return ans;
}

EdgeListGraph flip_graph(int n, EdgeListGraph g) {
  g = graph_cleanup(g);
  EdgeListGraph go;
  EdgeListGraph Kn = complete_graph(n);
  set_difference(Kn.begin(), Kn.end(), g.begin(), g.end(), back_inserter(go));
  return go;
}

EdgeListGraph filter_node_dec(const EdgeListGraph &g, int x) {
  EdgeListGraph ans;
  for (auto e : g) {
    if (e.first == x || e.second == x) continue;
    if (e.first > x) --e.first;
    if (e.second > x) --e.second;
    ans.push_back(e);
  }
  return ans;
}

EdgeListGraph filter_node(const EdgeListGraph &g, int x) {
  EdgeListGraph ans;
  for (auto e : g) {
    if (e.first == x || e.second == x) continue;
    ans.push_back(e);
  }
  return ans;
}

EdgeListGraph permute_graph(EdgeListGraph g, vector<int> perm) {
  for (auto &x : g) {
    x.first = perm[x.first];
    x.second = perm[x.second];
  }
  return g;
}

pair<EdgeListGraph, vector<int>> shuffle_graph(int n, EdgeListGraph g) {
  vector<int> perm(n, 0);
  for (int i = 0; i < n; ++i) {
    perm[i] = i;
  }
  shuffle(perm.begin(), perm.end(), mt);
  for (auto &x : g) {
    x = {perm[x.first], perm[x.second]};
  }
  return make_pair(g, perm);
}

vector<int> graph_isomorphic(int n, EdgeListGraph g1, EdgeListGraph g2) {
  g1 = graph_cleanup(g1);
  g2 = graph_cleanup(g2);
  vector<int> perm;
  for (int i = 0; i < n; ++i) {
    perm.push_back(i);
  }
  do {
    EdgeListGraph g11 = permute_graph(g1, perm);
    if (graph_cleanup(g11) == g2) {
      return perm;
    }
  } while (next_permutation(perm.begin(), perm.end()));
  return {};
}

unsigned popcnt(unsigned x) {
  unsigned ans = 0;
  while (x) {
    ans += (x & 1);
    x >>= 1;
  }
  return ans;
}

int max_deg(const SparseGraph &g) {
  pair<int, int> max_deg{-1, -1};
  for (int i = 0; i < g.size(); ++i) {
    max_deg = max(max_deg, {g[i].size(), i});
  }
  return max_deg.second;
}

namespace BigInt
{
  using u32 = uint32_t;
  using u64 = uint64_t;

  constexpr u32 bi_size = 2048;
  constexpr u32 bi_num = 2048 / 32;

  struct U2048
  {
    struct BitObject
    {
    private:
      u32 &ptr_;
      int pos_;
    public:
      BitObject(u32 &ptr, int pos): ptr_(ptr), pos_(pos) {
      }

      operator u32() const {
        return (ptr_ >> pos_) & 1;
      }

      u32 operator=(u32 v) {
        ptr_ &= ~(1u << pos_);
        ptr_ |= ((v & 1u) << pos_);
        return v;
      }
    };

    u32 val[bi_num];

    U2048(u32 v = 0) {
      memset(val, 0, sizeof val);
      val[0] = v;
    }

    U2048(const string &s) {
      memset(val, 0, sizeof val);
      for (int i = 0, j = 0, k = 0; i < s.size();
           i++, j++, k += j / 32, j %= 32) {
        val[k] += static_cast<u32>(s[i] - '0') << j;
      }
    }

    U2048(const vector<bool> &s) {
      memset(val, 0, sizeof val);
      for (int i = 0, j = 0, k = 0; i < s.size();
           i++, j++, k += j / 32, j %= 32) {
        val[k] += static_cast<u32>(s[i]) << j;
      }
    }

    u32 operator[](int x) const {
      return (val[x / 32] >> (x % 32)) & 1;
    }

    BitObject operator[](int x) {
      return BitObject{val[x / 32], x % 32};
    }

    string to_string(int bits) {
      string s;
      for (int i = 0; i < bits; ++i) {
        s += static_cast<char>('0' + operator[](i));
      }
      return s;
    }

    vector<int> bits_1() const {
      vector<int> ans;
      ans.reserve(bi_num);
      for (int i = 0; i < bi_size; i++) {
        if (operator[](i) == 1) {
          ans.push_back(i);
        }
      }
      return ans;
    }

    U2048 &operator+=(const U2048 &rhs) {
      u64 z = val[0];
      z += rhs.val[0];
      val[0] = z;
      z >>= 32;
      for (int i = 1; i < bi_num; ++i) {
        z += val[i];
        z += rhs.val[i];
        val[i] = z;
        z >>= 32;
      }
      return *this;
    }

    U2048 operator+(const U2048 &rhs) const {
      auto t = *this;
      t += rhs;
      return t;
    }

    U2048 operator-() const {
      auto t = *this;

      for (int i = 0; i < bi_num; ++i) {
        t.val[i] = ~ t.val[i];
      }
      return t + 1;
    }

    U2048 &operator-=(const U2048 &rhs) {
      return operator+=(-rhs);
    }

    U2048 operator-(const U2048 &rhs) const {
      return operator+(-rhs);
    }

    bool operator<(const U2048 &rhs) const {
      for (int i = bi_num - 1; i > 0; --i) {
        if (val[i] != rhs.val[i])
          return val[i] < rhs.val[i];
      }
      return val[0] < rhs.val[0];
    }

    bool operator<=(const U2048 &rhs) const {
      for (int i = bi_num - 1; i > 0; --i) {
        if (val[i] != rhs.val[i])
          return val[i] <= rhs.val[i];
      }
      return val[0] <= rhs.val[0];
    }
  };

  struct BinomTable
  {
    static const int size = 2048 + 1;
    U2048 *C[size];

    BinomTable() {
      memset(C, 0, sizeof C);
      for (int i = 0; i < size; i++) {
        C[i] = new U2048[min(i + 2, 100)];
      }
      C[0][0] = 1;
      for (int i = 1; i < size; ++i) {
        C[i][0] = 1;
        for (int j = 1; j <= i && j <= 97; ++j) {
          C[i][j] = C[i - 1][j - 1] + C[i - 1][j];
        }
      }
    }

    ~BinomTable() {
      for (int i = 0; i < size; i++) {
        delete []C[i];
      }
    }

    U2048 ord2set(U2048 x, int n, int k) {
      U2048 ans = 0;
      while (n > 0) {
        u32 bit = 0;
        if (k == 0 || C[n - 1][k - 1] <= x) {
          if(k > 0) {
            x -= C[n - 1][k - 1];
          }
          bit = 0;
        } else {
          bit = 1;
          --k;
        }
        ans[--n] = bit;
      }
      return ans;
    }

    U2048 set2ord(U2048 x, int n, int k) {
      U2048 ans = 0;
      while (n > 0) {
        u32 bit = x[n - 1];
        if (bit) {
          --k;
        } else {
          if (k > 0) {
            ans += C[n - 1][k - 1];
          }
        }
        --n;
      }
      return ans;
    }
  } c_table;
}

namespace Index
{
  struct TreeDFS
  {
    int n;
    int root;
    vector<bool> vis;
    SparseGraph g;
    using subtree_info = pair<string, vector<int>>;
    vector<subtree_info> subtree;

    static bool info_cmp(const subtree_info &a, const subtree_info &b) {
      if (a.second.size() != b.second.size()) {
        return a.second.size() < b.second.size();
      }
      return a.first < b.first;
    }

    TreeDFS(int _n, EdgeListGraph _g): n(_n), root(-1), vis(_n, false),
      g(graph_cast(_n, _g)), subtree(_n) {
      actual_work();
    }

    void dfs(int x, int p) {
      subtree_info info = {"(", {x}};
      vector<subtree_info> sons;
      for (auto y : g[x]) {
        if (y == p) continue;
        if (vis[y]) {
          throw -1;
        }
        vis[y] = 1;
        dfs(y, x);
        sons.push_back(subtree[y]);
      }
      sort(sons.begin(), sons.end(), info_cmp);
      for (auto son : sons) {
        info.first += son.first;
        copy(son.second.begin(), son.second.end(), back_inserter(info.second));
      }
      info.first += ")";
      subtree[x] = info;
    }

    subtree_info actual_work() {
      root = max_deg(g);
      fill(vis.begin(), vis.end(), false);
      try {
        dfs(root, root);
      } catch (int x) {
        return {};
      }
      return subtree[root];
    }

    subtree_info work() {
      return subtree[root];
    }
  };

  int index_n = 11;
  EdgeListGraph base_index = {
    {0, 1}, {0, 2}, {2, 3}, {0, 4}, {4, 5}, {5, 6}, {6, 7}, {7, 8}, {8, 9},
    {9, 10}
  };

  TreeDFS base{index_n, base_index};

  EdgeListGraph index_encode(int mask) {
    EdgeListGraph g;
    if (popcnt(mask ^ 1035) <= index_n / 2) {
      // mode 1
      g = base_index;
    } else {
      // mode 2
      g = flip_graph(index_n, base_index);
    }
    auto deg = deg_sequence(index_n, g);
    for (int i = 0; i < index_n; ++i) {
      if ((~((mask >> i) + deg[i])) & 1) {
        g.push_back({i, index_n});
      }
    }
    return g;
  }

  vector<int> index_decode(EdgeListGraph g) {
    g = graph_cleanup(g);
    if(g.size() >= 30) {
      g = flip_graph(index_n + 1, g);
    }
    SparseGraph gd = graph_cast(index_n + 1, g);
    int u = max_deg(gd);
    auto g1 = filter_node_dec(g, u);
    TreeDFS td(index_n, g1);
    auto [str, v] = td.work();
    if(v.empty() || str != base.work().first) return {};
    vector<int> ans(index_n + 1, -1);
    for (int i = 0; i < v.size(); ++i) {
      int t = v[i];
      if(t >= u) ++t;
      ans[t] = i;
    }
    ans[u] = index_n;
    return ans;
  }

  void test(int T) {
    while (T--) {
      if (T % 100 == 0) cout << T << endl;
      auto x = mt() % 2048;
      auto ge = index_encode(x);
      auto [g, tr] = shuffle_graph(index_n + 1, ge);
      auto v = index_decode(g);
      if (v.empty()) {
        cout << T<< " ERROR!!!!" << endl;
      } else {
        for (int i = 0; i < index_n + 1; ++i) {
          if (tr[v[i]] != i) {
            cout << "wrong " << i << endl;
          }
        }
      }
    }
  }
}

namespace Encoder
{
  EncoderResult graph_encode(EncoderParameter param, EdgeListGraph g,
                             vector<int> ids) {
    int n = param.labeled_n, k = param.lg2;
    int un = param.unlabeled_n; // n + k + 1

    vector<int> deg(un, 0);

    for (int i = 0; i < k; ++i) {
      for (int j = 0; j < n; ++j) {
        if ((ids[j] >> i) & 1) {
          g.push_back({i + n, j});
        }
      }
    }

    for (auto x : g) {
      deg[x.first]++;
      deg[x.second]++;
    }

    int u = k + n;
    for (int i = 0; i < n; ++i) {
      if (deg[i] % 2 != 0) {
        g.push_back({i, u});
      }
    }
    int mask = 0;
    for (int i = 0; i < k; ++i) {
      mask += (deg[i + n] % 2) << i;
    }
    EdgeListGraph index = Index::index_encode(mask);
    for (auto x : index) {
      g.push_back({x.first + n, x.second + n});
    }
    return EncoderResult{param, g};
  }

  EncoderParameter encode_param(int un) {
    assert(un == graph_size);
    return EncoderParameter{88, 100, 11, 519};
  }

  int encode_accept_len(EncoderParameter param) {
    int n = param.labeled_n;
    return n * (n - 1) / 2 + param.tab_len + 1;
  }

  EncoderResult encode(EncoderParameter param, vector<bool> str) {
    int n = param.labeled_n;
    EdgeListGraph g;
    auto it = str.begin();
    for (int i = 0; i < n; i++) {
      for (int j = i + 1; j < n; j++) {
        if (*it) {
          g.push_back({i, j});
        }
        ++it;
      }
    }
    vector<bool> ord_str(it, str.end() - 1);
    BigInt::U2048 ord{ord_str};
    // cerr << ord.to_string(106) << endl;
    auto sets = BigInt::c_table.ord2set(ord, 1 << param.lg2, n);
    // cerr << sets.to_string(128) << endl;
    auto convert = sets.bits_1();
    auto gout = graph_encode(param, g, convert);
    if (str.back()) {
      gout.g = flip_graph(param.unlabeled_n, gout.g);
    }
    return gout;
  }
};

namespace Decoder
{
  using Permutation = vector<int>;

  struct DecodeResult
  {
    vector<int> num;
    BigInt::U2048 num_set;
    vector<int> perm;
    bool flip;
  };

  namespace Test
  {
    bool is_permutation(Permutation perm) {
      sort(perm.begin(), perm.end());
      for (int i = 0; i < perm.size(); ++i) {
        if (perm[i] != i) return false;
      }
      return true;
    }
  }

  DecodeResult perm_decode(EncoderParameter param, EdgeListGraph ge) {
    int n = param.labeled_n;
    int un = param.unlabeled_n;
    SparseGraph g = graph_cast(un, ge);
    bool flip = false;

    int oddc = 0;
    map<int, int> odds;
    for (int i = 0; i < un; i++) {
      if (g[i].size() % 2 == 1) {
        odds[i] = oddc++;
      }
    }

    if (odds.size() > un / 2) {
      flip = true;
      ge = flip_graph(un, ge);
      g = graph_cast(un, ge);
      odds.clear();
      oddc = 0;
      for (int i = 0; i < un; i++) {
        if (g[i].size() % 2 == 1) {
          odds[i] = oddc++;
        }
      }
    }

    assert(odds.size() == param.lg2 + 1);

    EdgeListGraph odd_subgraph;
    for (int i = 0; i < ge.size(); ++i) {
      auto e = ge[i];
      if (odds.count(e.first) && odds.count(e.second)) {
        odd_subgraph.push_back({odds[e.first], odds[e.second]});
      }
    }

    auto index = Index::index_decode(odd_subgraph);

    for (auto &x : odds) {
      x.second = index[x.second];
    }

    vector<int> oddv(param.lg2 + 1, 0);
    for (auto x : odds) {
      oddv[x.second] = x.first;
    }
    int u = oddv[param.lg2];

    BigInt::U2048 num_set = 0;
    vector<int> num(un, 0);
    vector<int> perm(un, -1);
    for (int i = 0; i < param.lg2; ++i) {
      int x = oddv[i];
      for (auto y : g[x]) {
        num[y] += 1 << i;
      }
    }
    for (int i = 0; i <= param.lg2; ++i) {
      int x = oddv[i];
      num[x] = 114514;
    }

    map<int, int> num2id;
    for (int x = 0; x < un; ++x) {
      if (num[x] != 114514) {
        num2id[num[x]] = 0;
        num_set[num[x]] = 1;
      }
    }
    int cnt = 0;
    for (auto &id : num2id) {
      id.second = cnt++;
    }
    for (int x = 0; x < un; ++x) {
      if (num[x] != 114514) {
        perm[x] = num2id[num[x]];
      } else {
        perm[x] = odds[x] + n;
      }
    }
    return DecodeResult{num, num_set, perm, flip};
  }

  vector<bool> decode(EncoderResult res) {
    const auto &param = res.param;
    auto g = res.g;
    auto [num, num_set, perm, flip] = perm_decode(param, g);
#ifdef _DEBUG
    if (!Test::is_permutation(perm)) {
      throw exception("not a permutation -- perm_decode");
    }
#endif
    if (flip) g = flip_graph(param.unlabeled_n, g);
    auto gi = graph_cleanup(permute_graph(g, perm));
    vector<bool> ans(Encoder::encode_accept_len(param), false);
    int n = param.labeled_n;
    auto it = ans.begin();
    auto jt = gi.begin();
    for (int i = 0; i < n; i++) {
      for (int j = i + 1; j < n; j++) {
        pair<int, int> p = {i, j};
        while (jt != gi.end() && *jt < p) ++jt;
        if (jt != gi.end() && *jt == p) {
          *it = true;
        }
        ++it;
      }
    }
    // cerr << num_set.to_string(128) << endl;
    auto num_ord = BigInt::c_table.set2ord(num_set, 1 << param.lg2, n);
    // cerr << num_ord.to_string(106) << endl;
    for (int i = 0; i < param.tab_len; ++i) {
      *it++ = num_ord[i];
    }
    *it++ = flip;
    return ans;
  }
}

namespace Test
{
  bool test(EncoderParameter param) {
    int len = Encoder::encode_accept_len(param);
    vector<bool> arr(len, false);
    bernoulli_distribution bd;
    for (int i = 0; i < len; ++i) {
      arr[i] = bd(mt);
    }
    auto res = Encoder::encode(param, arr).g;
    vector<int> perm(param.unlabeled_n, 0);
    for (int i = 0; i < param.unlabeled_n; ++i) {
      perm[i] = i;
    }
    shuffle(perm.begin(), perm.end(), mt);
    for (auto &x : res) {
      x = {perm[x.first], perm[x.second]};
    }
    shuffle(res.begin(), res.end(), mt);
    res = graph_cleanup(res);
    auto dec = Decoder::decode(EncoderResult{param, res});
    return dec == arr;
  }
}

int main(int argc, char *argv[]) {
  //freopen("1.in", "r", stdin);
  //freopen("1.out", "w", stdout);
  cin.sync_with_stdio(false);
  cin.tie(nullptr);
  const auto param = Encoder::encode_param(graph_size);
  string s;
  cin >> s;
  if (s[0] == 'T') {
    int bound;
    cin >> bound;
    for (int i = 0; i < bound; ++i) {
      if (!Test::test(param)) {
        cout << "ERROR!" << endl;
      } else if (i % 100 == 0) {
        cout << i << endl;
      }
    }
  } else if (s[0] == 'N') {
    cout << Encoder::encode_accept_len(param) << endl;
  } else if (s[0] == 'A') {
    string input;
    cin >> input;
    vector<bool> arr(input.size(), false);
    transform(input.begin(), input.end(), arr.begin(), [](char c)
    {
      return c == '1';
    });
    auto g = Encoder::encode(param, arr).g;
    cout << g.size() << '\n';
    for (auto x : g) {
      cout << x.first + 1 << ' ' << x.second + 1 << '\n';
    }
  } else if (s[0] == 'B') {
    int e;
    cin >> e;
    EdgeListGraph g;
    g.reserve(e);
    for (int i = 0; i < e; ++i) {
      int u, v;
      cin >> u >> v;
      g.push_back({u - 1, v - 1});
    }
    auto arr = Decoder::decode({param, g});
    string output;
    transform(arr.begin(), arr.end(), back_inserter(output), [](bool c)
    {
      return c ? '1' : '0';
    });
    cout << output << '\n';
  }
  return 0;
}

namespace Trash
{
  int base_n = 7;
  EdgeListGraph base_graph = {{0, 1}, {0, 2}, {2, 3}, {0, 4}, {4, 5}, {5, 6}};

  EdgeListGraph base_graph1 = {
    {0, 1}, {0, 2}, {2, 3}, {0, 4}, {4, 5}, {5, 6}
  };

  vector<int> bad_set(int n, EdgeListGraph ge, vector<int> candidate) {
    auto gd = graph_cast(n, ge);
    vector<int> s;
    for (int i : candidate) {
      //// cerr << i << endl;
      EdgeListGraph gn = ge;
      for (int j = 0; j < n; ++j) {
        int deg = gd[j].size() + ((i >> j) & 1);
        if (deg % 2 == 0) {
          gn.push_back({j, n});
        }
      }
      bool bad = false;
      for (int j = 0; j < n; ++j) {
        EdgeListGraph gj = filter_node_dec(gn, j);
        if (graph_isomorphic(n, gj, ge).size()) {
          bad = true;
          break;
        }
      }
      if (bad) {
        s.push_back(i);
      }
    }
    return s;
  }

  int main() {
    vector<int> cand;
    for (int i = 0; i < (1 << base_n); ++i) {
      cand.push_back(i);
    }
    auto vec = bad_set(base_n, flip_graph(base_n, base_graph1), cand);
    for (auto x : vec) {
      cout << x << ",";
    }
    cout << endl;

    vector<int> perm;
    for (int i = 0; i < base_n; ++i) {
      perm.push_back(i);
    }
    do {
      auto base_graph2 = graph_cleanup(permute_graph(base_graph, perm));
      auto vec2 = bad_set(base_n, base_graph2, vec);
      vector<int> vec3;
      set_intersection(vec.begin(), vec.end(), vec2.begin(), vec2.end(),
                       back_inserter(vec3));
      if (vec3.size() == 1 && rand() % 50) continue;
      for (auto x : perm) cout << x;
      cout << ' ' << vec3.size() << endl;
      for (auto x : perm) cerr << x;
      // cerr << ' ' << vec3.size() << endl;
    } while (next_permutation(perm.begin(), perm.end()));
    return 0;
  }
}

EtaoinWu

题意

思考

算法想法

优化 #1

优化 #2

优化 #3

更多优化？

分析

代码