Reference:
- Renato F. Werneck, Design and Analysis of Data Structures for Dynamic Trees
- J. Holm, K. de Lichtenberg, and M. Thorup, Poly-logarithmic deterministic fully dynamic algorithms for connectivity, minimum spanning tree, 2-edge, and biconnectivity
- J. Holm and K. de Lichtenberg, Top-trees and dynamic graph algorithms
- Stephen Alstrup, Jacob Holm, Kristian De Lichtenberg, and Mikkel Thorup, Maintaining information in fully dynamic trees with top trees
注意这篇是笔记、不是教程,以后可能会出一份人类可读的版本。
本文的 Top tree 均指 multilevel participation 的实现。
本文不准备介绍操作复杂度定理的证明,因其过于复杂。
Top tree: 基于树的Contraction(暂译“合治”)的动态树。维护的是一个无向的森林。
将一棵树递归分成若干部分,top-down,称作“分治”;反过来的过程,bottom-up地把小块合并上来的过程,不妨称作“合治”。
Clusters
为了实现这一目标,我们需要设立合治的单位:cluster(暂译“树簇”,对应物似乎是“区间“之于序列数据结构)。这玩意需要满足以下条件:
- 有一个 \(O(1)\) 的边界(否则信息存不下)
- 可以合并拆分(废话)
- 不仅能储存树链信息,还可以储存”树块”信息(子树信息)
经过思考 查阅 ,树簇相关的术语被定义为如下:
- 树簇,简称簇:树上的一个连通子图,有至多两个点和全树的其他位置连接
- 这两个结点被称做界点 Boundary Node。 \(\mathcal C\) 的界点记作 \(\partial\mathcal C\) 。
- 不是界点的点被称做内点 Internal Node,记作 \(\mathcal C\setminus \partial{\mathcal C}\) 。
- 这两个界点之间的路径被称做簇路径 Cluster Path,记作 \(\pi(\mathcal C)\) 。
- 有一个界点的被称做叶簇(Leaf cluster),其余的称作路簇(Path cluster)
- 最小的(最基本的)簇是树的一条边,称作簇元 Edge cluster。“元”字取其基本元素之意,或译“簇素”,然其音有误解之可能。如果连接的是叶子与其他,那么有一个界点,称作 leaf edge cluster;反之有两个,称作 path edge cluster (不出现,不译)。
- 如果两个树簇 \(\mathcal A,\,\mathcal B\) 有且仅有一个公共点,(显然此时这个公共点是二者的公共界点),两个连通子图的并也是一个簇,那么他们被称做可合并(Mergeable),合并的结果记作 \(\mathcal A\cup \mathcal B\) 。
考察一下合并的几种可能形态。
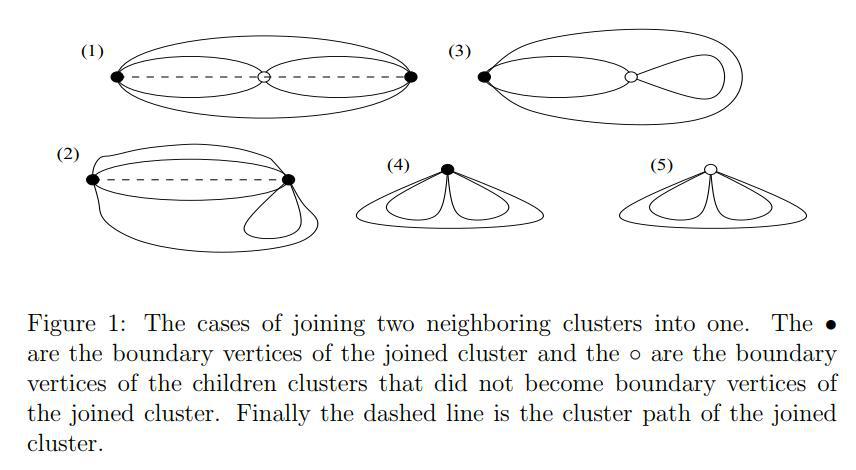
另外,由于我们的递归结构在顶层会遇到问题(并没有“向外的边”给全树这个簇用),引入一个叫 External Boundary Node 的概念(例外界点)。
此时我们就定义好了 top tree 的基本。
The Tree
那么这棵树是什么样子的呢?由于cluster是二合一合并,将其直接记录下来就好了。
- 一个簇对应一个结点
- 每个簇要么是叶子结点(簇元),要么是由两个簇合并起来,将他们作为大簇的孩子
- (父亲/祖先/后代定义略)
- 如果一个簇是另一个簇的父/子/祖先/后代,且他们的簇路径有至少一条边的交,那么分别称作path-ancestor/path-descendant/path-child。
于是就有了树结构。
我们考虑一下这棵树的若干性质。
- 一颗 Top tree 中,同一个点在一层只作为一个簇的内点。因此一个点只作为 $ O(n)$ 次内点。
- 另外,由于我们同时要讨论原树和 Top Tree,我将使用“簇”或“簇结点”指称 Top Tree上的结点。
The Operations, Black-box Flavored
那么这棵树支持什么操作呢?\(\def\defopname#1{{\newcommand{#1}{{\operatorname{#1}}}}}\def\opname#1{{\defopname{#1}\mathbf{#1}}}\)
\(\opname{Link}(v,w)\) :假设 \(v,\,w\) 两个结点在不同的树 \(\mathcal T_v,\,\mathcal T_w\)
中。建立一颗新的 Top Tree \(\mathcal
T\),代表 $T_v T_w {(u,v)} $ 。 \(\opname{Cut}(v,w)\):在 \(\mathcal T\) 中去除 \((v,w)\) 这条边,建立 \(\mathcal T_v\) 与 \(\mathcal T_w\) 。
\(\opname{Expose}(v,w)\) :将 \(v\) 与 \(w\) 设定为 \(\mathcal T\) 的例外界点。
这些操作暴露给外部,称作外部操作;是通过调用一系列内部操作来实现的。内部操作有以下这些:
\(\opname{Merge}(\mathcal A,\mathcal
B)\):将可合并簇 \(\mathcal A\)
与 \(\mathcal B\) 合并,创建 \(\mathcal C=\mathcal A\cup\mathcal B\)
作为他们的父簇,并 \(\partial\mathcal
C=\partial(\mathcal A\cup\mathcal B)\) 。设定 \(Info(\mathcal C):=\Merge(\mathcal C:\mathcal
A,\mathcal B)\),其中 \(\Merge(\mathcal
C:\mathcal A,\mathcal B)\) 是用户定义的计算信息合并的过程。
\(\opname{Split}(\mathcal C)\):其中
\(\mathcal C=\mathcal A\cup\mathcal
B\)。调用 \(\Split(\mathcal C:\mathcal
A,\mathcal B)\),然后把 \(\mathcal
C\) 从 \(\mathcal T\)
中删去。\(\Split(\mathcal C:\mathcal
A,\mathcal B)\) 是用户定义的用 \(Info(\mathcal C)\) 更新 \(Info(\mathcal A)\) 和 \(Info(\mathcal B)\)
的过程,可以理解为标记下传。
\(\opname{Create}((v,w))\):创建一条新边。调用同名用户定义过程。
\(\opname{Eradicate}(\mathcal
C)\):要求 \(\mathcal C\)
是一个簇元。删除这条边。调用同名用户定义过程。
这样,我们就可以把 Top tree 描述成一个黑盒:用户提供四个内部操作同名过程负责信息的维护,然后调用外部操作进行修改树结构,然后对根节点进行查询。
Usages
我们考虑这玩意的可能用途。
树形态的维护
\(\Link\) 和 \(\Cut\) 已经提供了。考虑 \(\opname{LCA}\) ,可以定义成 \(\opname{YCenter}(x,y,z)\) 表示这三个点所形成的 Y 字形的中间那个点。(待补)
Sone1
每个簇维护以下东西:
- 除簇路径外的内点 点权和、最大值、最小值
- 簇路径点权和、最大值、最小值
- 除簇路径外的内点 点权标记,可以写成 \(x\leftarrow kx+b\) 形式
- 簇路径点权标记,同理
在 \(\Merge\) 中处理加和、取 \(\operatorname{max}\) ,在 \(\Split\) 中把标记扔到两个孩子簇上。
(咦似乎这样甚至可以做子树/树链赋值,但是原题没有)
动态直径/中心类的
待补;见于 Non-local Search 部分。
The Construction
先不考虑维护信息,只考虑树结构。我们先考虑一个暴力的构建。事实上有人[citation needed]尝试过自顶向下的分治出一棵Top Tree来,不过似乎没有什么结果。我们考虑自底向上的构建:每次拿到一棵树,进行一些合并,合并完的cluster每个都作为一条边放到上层。在同一层一个簇只会被合并一次,因此这里簇等价于底层的边,以下将混用。
我们强行(随意地)给每个结点周围的边定一个极角序。这样,就可以定义出每条弧在顺向的前驱后继边;显然构成了一个边的循环欧拉序。
考虑两种基本的合并:Rake和Compress。
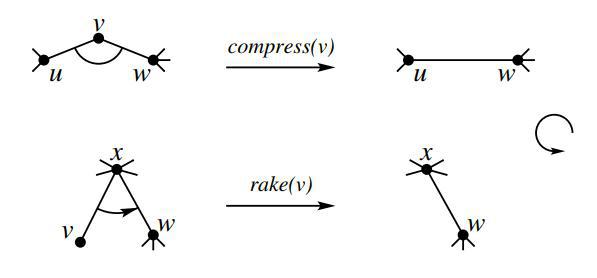
\(\opname{Rake}(x)\):\(x\) 是一个叶子结点;将 \(x\) 合并到他往上连的顺向边上去。 \(\opname{Compress}(x)\):\(x\) 是一个度为 \(2\) 的结点;将 \(x\) 两侧的边合起来。
对于每一层:使用一个数据结构(欧拉序循环链表)维护尚未被合并的簇;一开始每个簇没有父亲;然后遍历链表,随意地选择合法位置(指那些要合并的两条簇都没有父亲的)进行 \(\Rake\) 或 \(\Compress\),把结果作为两条簇的父亲;直到没有合法的位置为止。实现上,为了给每一个簇结点一个清晰的层次,可以给每一个孤儿建一个父亲,这个父亲没有其他孩子,且与孩子其维护的簇是相同的。然后,把所有父亲作为上一层的边使用。
然后操作层数(Top Tree的深度)就只有 \(O(\log{n})\) 了。这里的证明比较简单,分为三步:
- 读者自行验证:每棵树都有至少 \(\frac 12\) 的点度为1或2。
- 简单讨论一下,不难证明:每个 \(\Rake/\Compress\) 操作至多只会让两个相邻的原本合法的操作失效。
- 因此每层至少可以减少 \(\frac 16\) 的边。
- 事实上有一些反例违反了“每个 \(\mathrm R/\mathrm C\) 操作至多只会让两个相邻的原本合法的操作失效”,但我们可以证明,假设有 \(k\) 个反例,那么度为1或2的结点至少有 \(\frac 12 N+k\) 个。
然后这样我们就有一个 $ O(n)$ 的构建算法了,我们称作 \(\opname{Build}\)。在构建算法过程中,我们可以指定例外界点,以符合特殊需求。
The Operations, Detailed
现在来实现 \(\Link\) 和 \(\Cut\) 。我们先从暴力的方法来从 \(\mathcal T\) 构造出结果 Top Tree \(\mathcal T'\):
- 炸掉整棵树。
- 重新 \(\Build\) 。
- 在 \(\Build\) 的时候,每当“随意地选择合法位置”,改为“先选择 \(\mathcal T\) 中做过的、现在仍合法的决策,如果没有再随意选择”
这是一个正确性显然的做法,因为其得到的 \(\mathcal T'\) 仍然是一棵合法的(可能被 \(\Build\) 出来的)Top Tree。
来看复杂度证明。(我不准备给出完整的证明)我们只要证明,每层被影响到的、被重建的簇结点只有 \(O(1)\) 个。这很直观,但其证明非常复杂。完整正确的证明可见参考文献[1]。
现在考虑 \(\Link/\Cut\) 的具体实现。同样,只考虑树结构,不考虑簇信息的维护。
对于每一层:使用一个数据结构(欧拉序循环链表)维护尚未被合并的、被影响过的簇结点;一开始每个簇没有父亲;然后遍历链表,随意地选择合法位置(指那些要合并的两条簇都没有父亲的)进行 \(\Rake\) 或 \(\Compress\),把结果作为两条簇的父亲;直到没有合法的位置为止。最后,给每一个孤儿建一个父亲。然后,把所有父亲作为上一层的边使用。
(很显然,上文这段的撰写特意参照了 \(\Build\) 里面同样结构的一段。)
至于 \(\Expose\) ,\(\Expose(v,w)\) 的(一种可取)实现是这样的:我们把所有包含 \(v,\,w\) 作为内点的簇拿出来,炸掉、暴露出其内部结构(形成一个 \(O(\log n)\) 条边的临时树),然后拿构建算法去 \(\Build(\mathcal T:\partial\mathcal T=\{(v,w)\})\) 。
最后额外地来考虑信息的维护。事实上对于 \(\Link\) 和 \(\Cut\) 我们需要干的事情比较奇怪:我们先(虚的)做一遍上文描述的自底向上的东西,找到哪些结点要被 \(\Split\) 或 \(\Eradicate\) 掉,然后自顶向下地 \(\mathrm S/\mathrm E\) 它们,然后再自底向上地 \(\Create/\Merge\) 回来。
到这里,本体的做法就差不多讲完了。代码是不可能有的,这辈子都不可能写的。
Non-local Searching
如果,存在一个判定程序 \({B}:\mathrm{Cluster}\to \mathrm{Bool}\) ,可以判断出“寻找目标”在这个 Cluster 的哪一侧,那么存在一个 \(B\times O(\log n)\) 的算法可以找到我们的“寻找目标”。这是线段树上二分的简单推广。注意这个 \(B\) 的输入是根节点(整棵树),因此实现并非平凡。