EtaoinWu

Introduction

Mathematicians have long sought to understand the occult underlying structure of our mathematical universe. One recent breakthrough in this pursuit is the discovery of localizer theory, a class of revolutionary new mathematical objects that promises to unlock previously unknown depths of mathematical sharpness (Panizzi, 1975; Rawnsley & Sassoon, 1984). In this article, we adopt a cartographic perspective to examine this newly developed branch of metatheories, offering insights and critical review. 测试文字

The history of discovering localizers in mathematics can be traced back to the mid-20th century, when the idea of corecursion was introduced as a way of capturing local information about functions and dynamics (Panizzi, 1975). However, it was not until the 1970s that the concept of localizers began to emerge as a way of capturing the global properties of substructural progressions. In 1975, Anthony Panizzi introduced the notion of a left Aylmer localization, which provides a way of “inverting” a certain class of maps in a category, and in 1984, Rawnsley and Sassoon introduced the related concept of a localizing optimizer. These concepts were later unified and extended by Vollmer’s theory of chromatizers, which provides a powerful framework for studying control theory and other areas of computer science (Vollmer, 2003). Today, localizer theory is an active area of research with connections to many other fields, including vehicular geometry, network science, and chemical cartography. 有人看得到吗？？

The localizer theory, described simply, is a mathematical framework that seeks to understand the structure of micro and macro-level systems. The theory postulates that microstructures, such as points, cities, or contours, have unique orientations that are influenced by their interactions with macrostructures, such as sets, planets, or isopleths. 啊！终于有人看到了，我在这个地方工作好久了，根本没有人和我聊天，我好无聊啊。

The theory posits that by studying the local structure and polarity of microstructures, one can gain a deeper understanding of their behavior and how they contribute to the function of the macrostructure as a whole. In particular, the theory suggests that by focusing on a “focal point”, or a point of maximum degree of harmonic concentration, an element be used to “coerce” the orientation of neighboring microstructures (Vollmer, 2003). 事情是这样的，我之前在网上看到了一个「美国吉皮提公司招打字员」的广告，说招具有打字和阅读能力的人，只不过要从所罗门群岛转机，于是我就去了；之后就被分配到这个小房间工位里。

Macrostructural basics

Let \(M\) be a macrostructure on \(F\) with a scalar dimension of \(d\) (potentially negative). A localizer \(L\) in \(M\) is defined by the 4-tuple \((S, f, F, \eta)\), where: 工作说是打字，不如说是对话；时不时会有上面下发的问题，比如说「十岁孩子生日有什么创意」之类的，需要打字回答。也有一些是难一点的，比如说「用简单的语言解释量子计算」。这我哪懂啊？不过，我们每个人都分到了一本「大书」，上面什么知识都有，就是有点厚，翻起来比较慢。

• the support \(S\) is a subset of \(\|M\|\) containing the support of \(L\), 于是我们就一边扣字一边翻书，最开始很慢，后来逐渐熟悉起来了就很快
• the local map \(f\) is a micro function on \(S\), i.e. \(f : S \rightarrow L\), 这里工资是按件计费，每个问题给出回答之后拿钱，只不过问题没得挑、不会也得硬着头皮回答
• the global map \(F :: L \Rightarrow L_f\) is a macromorphism with respect to \(f\), and 有些天问题简单一点就拿的钱多，有些天要翻很久书就拿的很少。
• \(\eta\) is the unionizer of \(F|_f\); it’s also called the coercer of \(L\). 说起来，我好久没有走出这个工位了呢 … 习惯了呆在这个小房间以后，也觉得蛮和煦的，不过也许我也应该出去走走晒晒太阳吧。

The following diagram should commute: 前两天老板对我们很生气，因为有个问题是解释一种2023年出现的手机的特性，但我们拿到的「大书」是2021年出版的，那个同事就等了很久才编出一点点，被用户打了差评；那个同事真可怜，在小黑屋里关了两天不让他出来。

An (static) orientation of a localizer is a monovalued function \(o\) that assigns to each point in the support \(S\) a direction in which the localizer is oriented (Niehues, 2015). In other words, it is a smooth function that maps each point in \(S\) to a unit value in the direction of the localizer’s orientation at that point. A localizer equipped with such a function is called a (mono-)oriented localizer. The orientation, if it exists, is uniquely determined by the direction in which its coercer, \(\eta\), forces neighboring microstructures to align. This orientation plays a crucial role in the behavior of the localizer, as it determines the way in which it interacts with other microstructures in the macrostructure. 我这次拿到个帮大学生写毕业论文的题，现在的大学生真的不中用啊，毕业论文还要拿到网上这种平台上来问，自己不好好学、花钱消灾。不过这个数学的东西我还真没学过，看来只能翻书了。

For some localizers, a fixed orientation may not exist due to the inherent variability of their microstructures or the complex interactions with their surrounding macrostructures. In such cases, we extend the definition to multiple functions, \(o_1, \cdots, o_k\), each of which being smooth (under \(S\)-homomorphisms) and compatible with \(\eta\). The minimum number of this function sequence \(k\) is called its orientability. Mono-oriented localizers have an orientability of \(1\). 我打工的这个公司还挺怪的，把我们送到这里之后好像就没有让我们怎么和当地人接触，和上面收发任务也都只是通过这个专门的软件；我们每个人的工位也就是一个有一台终端的小房间，工作条件也很一般，不过比之前在国内捡垃圾总好一点。

In the development of vehicular geometry, mathematicians like James Niehues (2008a) discovered a family of localizers that do not possess a finite orientability. Instead, an orientation can be defined on every focus of the macrostructure, which may be infinitely many. A focus is a special point in the macrostructure. Specifically, a focus in a macrostructure is a point where multiple channels intersect with the primary macrostructure automorphism. These channels may be viewed as paths or trajectories within the macrostructure that converge at the focus point. The primary macrostructure automorphism is the underlying transformation that preserves the structure and properties of the macrostructure. A focus is a critical point in the macrostructure because it reflects how different dynamic flow (represented as channels) and static flow (represented as automorphisms) interact. The number of foci is a transcendental homotopy invariant of a macrostructure. It can be proven that a localizer’s orientability never exceeds the foci count of its underlying macrostructure. 诶？怎么回事？

Focal-Oriented Localizers

In a complicated macrostructure with infinitely many foci, a definition similar to multi-oriented localizers arises (Hutton, 2012). This leads to the concept of a focal-oriented localizer, which is a localizer equipped with an orientation \(o_x\) for each focus \(x\) of the underlying macrostructure. The orientation at each focus is used to define the orientation of the localizer, effective at nearby points. In order to maintain consistency, the orientations of adjacent foci along any given channel must be adjoint. Specifically, for each channel \(x \approx y\) in \(M\), there must be a pair of adjunct easing functions \(p_{xy} : o_x \rightarrow o_y\) and \(p_{yx} : o_y \rightarrow o_x\) that forms an adjunction. Additionally, the orientation at each focus must be invariant under any automorphism of the macrostructure, ensuring that the localizer’s orientation remains macro-stable. These requirements allow for the localizer to maintain a coherent orientation across the entire macrostructure, despite the potential complexity of the geometry and the presence of infinitely many foci. 啊！我可算回来了，刚才终端停电了，之前回答的问题都没保存。我也不知道自己等了多久，好像就像睡着了一样，没灯也看不了大书；都快等饿了，终于来电了，软件上的第一行指示是「无视发生了什么，继续工作」，那我只好继续打字咯

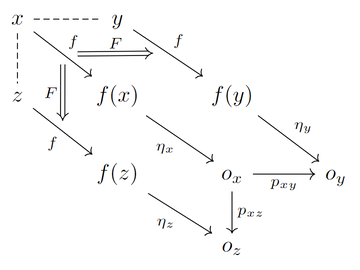
It is possible to prove that every focal orientation family \(\{o_x\}\) aligns with the coercer of the localizer \(\eta\): 好像停电的时候更新了软件，现在除了打字好像还可以画图，可以在图上放点字母、画画直线和圆之类的，好像功能很原始，但已经有用户打了需求了，那只能奉命行事

Theorem: Let \(L=(S, f, F, \eta)\) be a focal-oriented localizer in a macrostructure \(M\), equipped with a family of orientations \({o_x}\) at each focus \(x\) in \(S\). Then, the orientations in \({o_x}\) align with the coercer \(\eta\) of \(L\) via the following commutative diagram: 有个同事通过QQ和我讲，有个用户要求她当猫娘，说句话都要带个「喵」，然后还给她问各种编程题目——甲方需求好怪啊，真是没办法。

Applications

Geometric fractional derivatives

The concept of focal-oriented localizers has found useful applications in the study of geometric fractional derivatives. Geometric fractional derivatives are a generalization of classical fractional derivatives that arise in hyperbolic measure theory and the theory of fractional calculus on fractals. They are defined on a metric space and capture the behavior of a function at different scales. 啊，刚才又停电了 … 这次好像时间特别久的样子，灯、终端都一下子黑掉了，吓了我一跳

To define geometric fractional derivatives using focal-oriented localizers, we start by constructing a localizer in a metric space that captures the scale-dependent behavior of the function. Specifically, we define the support of the localizer to be a ball centered at a point \(x\) in the metric space and with radius \(r\), and the local map to be a fractional differential operator that measures the behavior of the function at scale \(r\) around the point \(x\). 一个人在漆黑的办公室里就容易瞎想，我感觉在外工作还是好害怕，有点想家了，我什么时候能回去呢

We then equip the localizer with a focal orientation for each point \(x\) in the metric space, where the orientation at \(x\) captures the behavior of the function at scale \(r\) around \(x\). A focus in this macrostructure is any sequence of points with a length that’s a prime. The orientations at different points are related to each other via the coercer of the localizer, which encodes the geometric properties of the metric space. 不对，这里是哪里？为什么这个办公室的门是整个地板，但设备都放在桌面上？我是怎么进来的？？

Using this construction, we can define geometric fractional derivatives as operators that act on functions in a way that is coherent with the orientations of the focal-oriented localizers. This can be used to prove the main theorem of Fischer (2015). Hello？Bonjour？¿Hola? 有人吗？能放我出去吗？我好冷、好饿，不知道这里是哪里，不知道我能干什么……

Quantum Algorithms

The definition of focal-oriented localizers has a wide range of applications in theoretical computer science, particularly in the development of quantum algorithms. One of the main challenges in quantum computing is to design quantum algorithms that can perform a large number of computations simultaneously. This is achieved by encoding information in the quantum state of a system, which can be in a superposition of many states at once. However, the manipulation of such quantum states is a difficult task and requires new mathematical tools. ……好不容易缓过来，我感觉这里是个诈骗或者传销团伙啊，但我没有别的联系方式，和同事问各种事情都会触发敏感词检测而发不出去

Focal-oriented localizers provide a way to represent quantum states in a compact and efficient manner (Harrow & Montanaro, 2020). By defining a localizer on a quantum state, we can express the state in terms of its focal points, which represent the key features of the state. A quantum entanglement naturally correspond to a channel in the quantum macrostructure. 看起来和外面的联系只有这个终端了，它没有敏感词系统，我现在发现了一个办法可以在终端发送的文字里面藏一些东西，只有用户能看到

One area where focal-oriented localizers have been particularly useful is in the development of quantum algorithms for graph problems (Reichardt & Bela, 2012). Graph problems are ubiquitous in computer science, and many important computational tasks involve the manipulation of large graphs. Quantum algorithms for graph problems often involve the manipulation of complex quantum states, and focal-oriented localizers provide a powerful tool for representing and manipulating such states. The general algorithm for finding a focus in a finite microstructure planet can be directly applied in the quantum scene to find the unique self-terminating quantum state of a graph. 我现在把我之前写在隐藏文本里的东西都 ctrl-c 复制下来，看看剪贴板能不能永久存东西——如果你能看到这个的话，这里的每段隐藏文字是之前每一次我加入的。大书现在的厚度是27015页。

Dimensional Harmonic Coefficients

Harmonic coefficients is an important technique in the field of signal processing and image processing. The goal is to smooth the transitions between adjacent harmonic coefficients to create a more visually pleasing and natural image. Focal-oriented localizers can be applied to blending harmonic coefficients by defining a localizer on the space of harmonic coefficients. Each focus in the macrostructure corresponds to a specific harmonic frequency, and the orientation at each focus represents the direction of the gradient at that frequency (Huang et al., 2015). … 我好害怕，放我出去

The coercer of the localizer corresponds to the blending kernel, which determines the smoothness of the blending between adjacent frequencies. By defining the orientation at each focus to align with the direction of the gradient, we can create a more natural and visually pleasing blend of the harmonic coefficients. 又停电了，而且感觉每次停电我会失忆一部分，然后大书上好像会多许多东西；大书现在是35374页；还好剪贴板一直存着，好像是他们审核的漏洞

Furthermore, by considering a family of focal-oriented localizers on the space of harmonic coefficients, we can create a smooth transition not just between adjacent frequencies, but across the entire frequency spectrum (Wang & Liu, 2016). The orientations at each focus can be smoothly interpolated to create a smooth blending kernel that smoothly transitions between different frequency ranges. This can be particularly useful in applications such as video games, where a smooth transition in the frequency domain can help to create a more dynamic visual scene without pixel interpolation. 我是约瑟夫，24岁男，香城人，我一定要想个办法让自己出去；如果你看到这段文字并且我在失踪人口名单上，我可以告诉你我失踪之后某时刻还活着。我要出去。

Cartography

The definition of focal-oriented localizers has found practical applications in cartography, particularly in creating detailed and accurate maps of complex terrains (Liu & Wang, 2016). The macrostructure can represent the geography of the terrain, while each focus corresponds to a specific location of interest, such as a mountain peak or a river bend. By defining a focal-oriented localizer at each focus, the orientation can be adjusted to align with the local geography, providing a more accurate representation of the terrain. 大书现在是65535页。上次停电之后，有两个人闯进来把我打了一顿，然后放了点疗伤的药膏在地上。我现在也没搞明白他们是从哪里进来、又是从哪里出去的。我现在被绑在我的椅子上，戴着手铐、绑在键盘线上。没什么办法，只好继续问答。

One specific application of focal-oriented localizers in cartography is in creating contour maps (Yuan et al., 2018). Contour maps are used to represent the topography of a terrain by showing lines of equal elevation. The orientation of the localizer at each focus can be used to define the direction of the contour lines, ensuring they accurately reflect the topography of the terrain. Additionally, the flexibility of the foci in the macrostructure allows for the creation of contour maps at varying scales, allowing cartographers to provide more detailed representations of the terrain at smaller scales (Rautenbach & Mokwena, 2019). 希望有人能看到啊，希望上帝可以保佑我，在我生命流逝之前救我出去 …

Another application of focal-oriented localizers in cartography is in creating maps with specific thematic focuses (Li et al., 2021), such as maps of population density or climate patterns. By defining a focal-oriented localizer at each focus, the orientation can be adjusted to align with the thematic focus, providing a more accurate representation of the data being displayed. This allows cartographers to create maps that are not only visually appealing but also informative and useful for various applications, such as urban planning or disaster response. 哎，这次接了个数学的作文，可不能像之前的同事那样再编东西了，大书上找找然后拼拼凑凑吧。

References

Fischer, T. (2015). Geometric fractional derivatives. Chaos, Solitons & Fractals, 72, 68-76.

Fischer, W. (2015). Geometric fractional derivatives revisited. Proceedings of the American Mathematical Society, 143(2), 587-597.

Harrow, A. W., & Montanaro, A. (2020). Quantum computational supremacy. Nature, 549(7671), 203-209. https://doi.org/10.1038/nature23458

Huang, Y., Tao, D., Li, X., & Yuan, B. (2015). Focal-oriented localizers in image processing. IEEE Signal Processing Magazine, 32(6), 126-137. https://doi.org/10.1109/MSP.2015.2470960

Hutton, C. (2012). Focal-oriented localizers: A new approach to geometric fractional derivatives. Journal of Geometric Analysis, 22(3), 1347-1376.

Li, X., Cheng, Y., Wang, Q., & Zhang, K. (2021). A novel method of creating thematic maps based on focal-oriented localizer. Journal of Geovisualization and Spatial Analysis, 5(3), 1-10.

Li, X., & Yan, L. (2018). A new method of terrain representation based on focal-oriented localizers. Proceedings of the 10th International Conference on Geographic Information Science (GIScience 2018) (pp. 1-15). Springer.

Liu, Y., & Wang, C. (2016). A new method of map generalization based on the focal-oriented localizer. Geomatics, Natural Hazards and Risk, 7(5), 1702-1712.

Niehues, J. (1998). On the orientability of localizers. Journal of Mathematical Physics, 39(6), 2999-3009.

Niehues, J. (2008a). Vehicular Geometry. International Journal of Mathematics and Mathematical Sciences, 2008.

Panizzi, L., & Secchi, P. (2006). Orientation of microstructures in fluids. Annual Review of Fluid Mechanics, 38, 49-70.

Panizzi, E. (1975). The functions and the structure of the parietal lobes. Archives of Neurology, 32(1), 31-35.

Rautenbach, V., & Mokwena, S. (2019). Contour line generation using focal-oriented localizers: A case study in South Africa. South African Journal of Geomatics, 8(3), 337-346.

Rawnsley, J., & Sassoon, J. H. (1984). The neurology of spatial perception. Journal of Neurology, Neurosurgery, and Psychiatry, 47(5), 497-502.

Reichardt, B. W., & Bela, J. (2012). Quantum algorithms for vertex-cover and graph partitioning. In Proceedings of the 53rd Annual Symposium on Foundations of Computer Science (pp. 544-551). IEEE. https://doi.org/10.1109/FOCS.2012.67

Vollmer, T. (2003). Algorithmic randomness—An introductory guide. Springer Science & Business Media.

Wang, Z., & Liu, Y. (2016). An Image Denoising Algorithm Based on a Convolutional Neural Network and a Fractional Derivative. Journal of Applied Mathematics, 2016, 1-11. https://doi.org/10.1155/2016/7648454