欧拉回路树

（你看到的是2019/9/19的 revision）

缘起

当年 naive 的 EtaoinWu 在网上看了一些奇奇怪怪的东西，就写了这篇东西来讲一讲。现在发现小坑真的多，就来改一改再拿出来。这个数据结构可以用于维护子树信息，但无法简单地维护树链信息；由于比 multi-level partition top tree 简短，因此可以拿来做动态图连通性。

ETT 简介

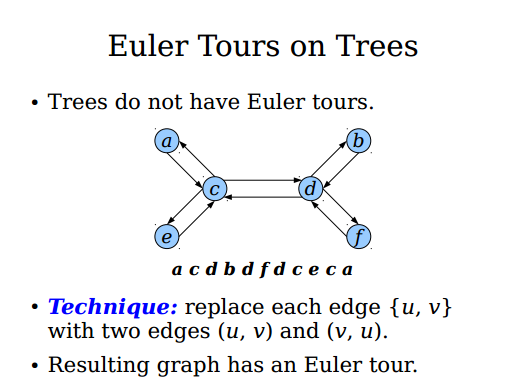
树 (无根树, 即没有环的联通无向图) 正常情况下没有欧拉回路, 但是把每条无向边{u,v}变为一条(u,v)的有向边与一条(v,u)的有向边之后, 就具有了欧拉回路, 定义这个欧拉回路为“树的欧拉回路”. 伪代码如下:

void euler_tour(node *now) {
    print(now->data)
    for(son in now.sons) {
        euler_tour(son)
        print(now->data)
    }
}

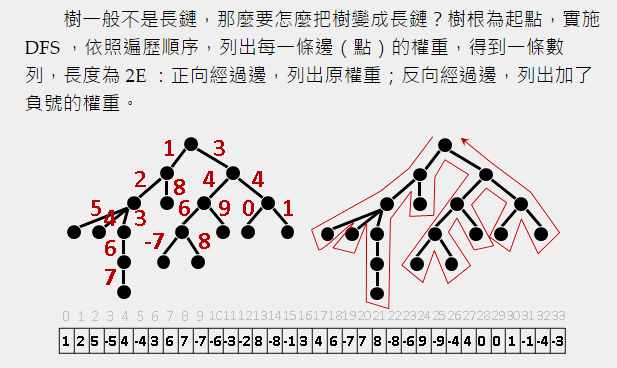
使用这样的方式, 就可以将树转化为一条链, 长度小于等于 2n. 而维护原来的树, 可以转化为维护这个欧拉回路. 维护一条链是相对简单的任务，有各种东西可以完成，比如平衡树。

首先, 让我们分析一下 link & cut & is_connected 在 Euler tour 上的影响.

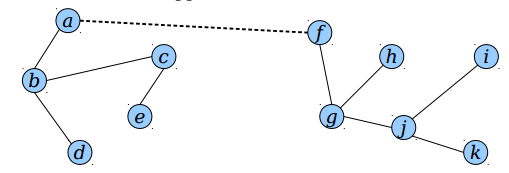
link

首先看link. 上图中虚线连接的两棵树的欧拉回路分别是a b d b c e c b / f g j k j i j g h g, 执行link(a,f) 而得到的新树的欧拉回路是a b d b c e c b a f g j k j i j g h g f, 就是将二者直接合并起来. 这里用到了区间合并的操作.

请注意, 这里的欧拉回路中删去了最后一个, 仅仅为了代码方便
事实上这是体现了 用边来维护欧拉序的意义下 每条边的始点的位置
比如, 上图虚线左侧的树的欧拉回路 (利用上述伪代码) 得到的应该为a b d b c e c b a 
但是这个回路的第一项与最后一项是相同的, 直接将最后一项删除以便维护. 这也更符回路的定义.

而如果上述树是b a b c e c b d / j k j i j g h g f g, 那么把两个回路的任意一个 a/f节点找出来, 在它们之前将它们断开 (A=b / B=a b c e c b d / C=j k j i j g h g / D=f g ) , 新建a与f, 然后按A newa D C newf B的顺序连接起来, 得到b a f g j k j i j g h g f a b c e c b d, 这与前段得到的树是一样的.

而split一个线段、merge两个线段的复杂度取决于我们储存Euler Tour的数据结构.

cut

至于cut, 就用刚才那个link的逆过程吧. 对于在根上的cut, 一开始是a b d b c e c b a f g j k j i j g h g f, 直接断开中间的a与f, 得到的就是原来的那两个回路a b d b c e c b / f g j k j i j g h g.

对于不在根上的cut, 比如在b a f g j k j i j g h g f a b c e c b d上执行cut(a,f), 首先要找到回路中a f的位置与f a的位置, 然后将这两个位置断开, 得到b a f g j k j i j g h g f a b c e c b d, 将断开位置左侧的两个点删去, 得到A=b B=f g j k j i j g h g C=a b c e c b d, 然后将A与C合并, 就得到了新的两棵树.

is_connected

判断两者是否联通, 就等于是判断二者是否在同一个欧拉回路内. 直接找到一个节点的任意一个node, 然后走到根 \(O(\log n)\), 如果root相同那么就在一个联通块中.

实现细节

观察以上文中我使用了斜体的地方, 这些地方指示了我们需要做出哪些索引工作:

找到一个树中节点在ETT中的任意一个点
找到两个点之间的位置, 即: 找到一条树中的边在ETT中的位置

所以, 我们有了以下两种方案:

对于每个 ETTNode, 存储原图上的一个边. 然而这样就没法找节点, 那么有一个小trick: 为每一个点增加一个自环, 仍然维护欧拉回路, 存储完毕之后使用二叉树或者哈希做索引；
对于每个 ETTNode, 储存原图上的一个点, 一个点就有多个位置, 索引数组使用vector<map<int, node *>>, v[i][j]表示储存了i的值、欧拉回路上后继是j号节点的那个node, 这样实现比较好写, 空间常数较小.

最后实现

最终代码里使用了非旋转 Treap 做储存欧拉回路的平衡树, 非旋转 Treap 使用的 merge / split 操作正好适合ETT的作用.

代码很长，也可以在 LOJ#122 上找到代码；各路神仙有自己的写法，可以参照着看，我的实现并不特别优秀。

[SDOI2008]洞穴勘测裸题程序

显然, 这题可以LCT做, 但是也可以当做一道ETT的题. 代码如下: (常数大2~3倍)

#include <bits/stdc++.h>
using namespace std;

struct fastIO {
    static const int BUF_SIZE = 1 << 15;
    char inbuf[BUF_SIZE];
    char outbuf[BUF_SIZE];
    int incur, outcur;
    FILE *in, *out;
    fastIO():incur(BUF_SIZE),outcur(0),in(stdin),out(stdout) {}
    fastIO(const fastIO &iio):incur(BUF_SIZE),outcur(0),in(iio.in),out(iio.out) {}
    ~fastIO() {close();}
    inline fastIO &operator=(const fastIO &iio) {incur = (BUF_SIZE),outcur = (0),in = (iio.in),out = (iio.out);return *this;}
    inline char getchar() {if (incur == BUF_SIZE) {fread(inbuf, BUF_SIZE, 1, in);incur = 0;}return inbuf[incur++];}
    inline void getstr(char *str) {*str = getchar();while(!isgraph(*str))*str = getchar();while(isgraph(*str))*++str = getchar();*str = 0;}
    inline int getint() {int x = 0;char c = getchar();while (!isdigit(c))c = getchar();while (isdigit(c)) {x = x * 10 + c - '0';c = getchar();}return x;}
    inline void putchar(char ch) {outbuf[outcur++] = ch;if (outcur == BUF_SIZE) {fwrite(outbuf, BUF_SIZE, 1, out);outcur = 0;}  }
    inline void putint(int x) {if (x >= 10) putint(x / 10);putchar(x % 10 + '0');}
    inline void close() {if (outcur > 0) fwrite(outbuf, outcur, 1, out);outcur = 0;}
} IO;
unsigned long rng(unsigned long e = 0)
{
    static unsigned long t = 0, x = 123456789, y = 362436069, z = 521288629, w = 88675123, v = 5783321, d = 6615241;
    d += e; x += d; t = (x ^ (x >> 2)); x = y; y = z; z = w; w = v; v = (v ^ (v << 4)) ^ (t ^ (t << 1));
    return e ? (((d += 362437) + v) % e) : ((d += 362437) + v);
}
struct EulerTourTree {
    struct node {
        node *lch = nullptr;
        node *rch = nullptr;
        node *parent = nullptr;
        int size = 1;
        int vid;
        bool active = false;
        int sub = 0;
        node(int vid) : vid(vid) {}
    };

    unsigned long long xor_shift() {
        static unsigned long long x = time(NULL);
        x ^= x << 13; x ^= x >> 7; x ^= x << 17;
        return x;
    }

    size_t size(node *x) {
        return x != nullptr ? x->size : 0;
    }

    size_t sub(node *x) {
        return x != nullptr ? x->sub : 0;
    }

    node *update(node *x) {
        if (x == nullptr) return x;
        x->size = 1 + size(x->lch) + size(x->rch);
        x->sub = sub(x->lch) + sub(x->rch);
        if (x->active) x->sub++;
        return x;
    }

    void update_ancestor(node *x) {
        if (x == nullptr) return;
        x = update(x);
        update_ancestor(x->parent);
    }

    void activate(node *x, bool value) {
        if (x == nullptr) return;
        x->active = value;
        update_ancestor(x);
    }

    node *merge(node *x, node *y) {
        if (x == nullptr) return y;
        if (y == nullptr) return x;
        if (xor_shift() % (size(x) + size(y)) < size(x)) {
            x->rch = merge(x->rch, y);
            if (x->rch != nullptr) x->rch->parent = x;
            return update(x);
        } else {
            y->lch = merge(x, y->lch);
            if (y->lch != nullptr) y->lch->parent = y;
            return update(y);
        }
    }

    pair<node *, node *> split(node *x, size_t k) {
        if (x == nullptr) return make_pair(nullptr, nullptr);
        if (k <= size(x->lch)) {
            auto p = split(x->lch, k);
            x->lch = p.second;
            if (p.first != nullptr) p.first->parent = nullptr;
            if (p.second != nullptr) p.second->parent = x;
            return make_pair(p.first, update(x));
        } else {
            auto p = split(x->rch, k - size(x->lch) - 1);
            x->rch = p.first;
            if (p.first != nullptr) p.first->parent = x;
            if (p.second != nullptr) p.second->parent = nullptr;
            return make_pair(update(x), p.second);
        }
    }

    node *root(node *x) {
        if (x == nullptr) return x;
        if (x->parent == nullptr) return x;
        return root(x->parent);
    }

    int index_of(node *x) {
        if (x == nullptr) return 0;
        int result = -1;
        bool l = true;
        while (x != nullptr) {
            if (l) result += 1 + size(x->lch);
            if (x->parent == nullptr) break;
            l = x->parent->rch == x;
            x = x->parent;
        }
        return result;
    }

    void connected_component(node *x, vector<int> &res) {
        if (x == nullptr) return;
        if (x->active) res.push_back(x->vid);
        connected_component(x->lch, res);
        connected_component(x->rch, res);
    }

    vector<int> connected_component(int u) {
        node *x = root(any_node(u));
        if (x == nullptr) return{ u };
        vector<int> res;
        connected_component(x, res);
        return res;
    }

    vector<map<int, node *>> tr;

    EulerTourTree(int n) : tr(n) {}

    node *any_node(int u) {
        return tr[u].empty() ? nullptr : tr[u].begin()->second;
    }

    bool link(int u, int v) {
        node *x = any_node(u);
        node *y = any_node(v);

        node *root_x = root(x);
        node *root_y = root(y);

        if (root_x != nullptr && root_x == root_y) return false;

        node *A, *B, *C, *D;
        tie(A, B) = split(root_x, index_of(x));
        tie(C, D) = split(root_y, index_of(y));

        // AB, CD => A (u->v) D C (v->u) B

        node *uv = new node(u);
        node *vu = new node(v);

        if (tr[u].empty()) activate(uv, true);
        if (tr[v].empty()) activate(vu, true);

        tr[u][v] = uv;
        tr[v][u] = vu;

        A = merge(A, uv);
        A = merge(A, D);
        A = merge(A, C);
        A = merge(A, vu);
        A = merge(A, B);

        return true;
    }

    bool cut(int u, int v) {
        if (tr[u].count(v) == 0) return false;
        node *uv = tr[u][v];
        node *vu = tr[v][u];
        tr[u].erase(v);
        tr[v].erase(u);

        if (uv->active) {
            activate(uv, false);
            activate(any_node(u), true);
        }
        if (vu->active) {
            activate(vu, false);
            activate(any_node(v), true);
        }

        node *rt = root(uv);

        int index_uv = index_of(uv);
        int index_vu = index_of(vu);

        if (index_uv > index_vu) swap(index_uv, index_vu);

        node *A, *B;
        auto p = split(rt, index_vu);
        B = split(p.second, 1).second;
        auto q = split(p.first, index_uv);
        A = q.first;
        auto r = split(q.second, 1);
        merge(B, A);

        return true;
    }

    bool is_connected(int u, int v) {
        if (u == v) return true;
        node *x = any_node(u);
        node *y = any_node(v);
        return x != nullptr && root(x) == root(y);
    }

    int sub(int u) {
        node *x = any_node(u);
        if (x == nullptr) return 1;
        return sub(root(x));
    }
};

char c[1111];
signed main()
{
    int n,m;
    n = IO.getint();
    m = IO.getint();
    EulerTourTree ETT(n+1);
    for (int i = 1; i <= m; i++) {
        int a1, b1;
        IO.getstr(c);
        a1 = IO.getint();
        b1 = IO.getint();
        if (c[0] == 'Q') {
            printf((ETT.is_connected(a1,b1))?"Yes\n":"No\n");
        } else if (c[0] == 'C') {
            ETT.link(a1, b1);
        } else if (c[0] == 'D') {
            ETT.cut(a1, b1);
        }
    }
    return 0;
}

EtaoinWu

缘起

相关参考资料